题目内容
在Rt△ABC中,AB⊥AC,AD⊥BC于D,求证:| 1 |
| AD2 |
| 1 |
| AB2 |
| 1 |
| AC2 |
分析:利用平面中的射影定理证明;将平面中的三角形类比成空间的三棱锥,三角形的两边垂直类比成三棱锥的三棱垂直,得到类比性质
通过作辅助线将空间的证明问题转化为三角形中的性质.
通过作辅助线将空间的证明问题转化为三角形中的性质.
解答:
 解:如图(1)所示,由射影定理知AD2=BD•DC,AB2=BD•BC,AC2=BC•DC,
解:如图(1)所示,由射影定理知AD2=BD•DC,AB2=BD•BC,AC2=BC•DC,
∴
=
=
=
.
又BC2=AB2+AC2,
∴
=
=
+
.
所以
=
+
.
类比AB⊥AC,AD⊥BC猜想:
四面体A-BCD中,AB、AC、AD两两垂直,
AE⊥平面BCD,则
=
+
+
.
如图(2),连接BE交CD于F,
连接AF.∵AB⊥AC,AB⊥AD,
∴AB⊥平面ACD.
而AF?平面ACD,∴AB⊥AF.
在Rt△ABF中,AE⊥BF,
∴
=
+
.
在Rt△ACD中,AF⊥CD,
∴
=
+
.
∴
=
+
+
,故猜想正确.

 解:如图(1)所示,由射影定理知AD2=BD•DC,AB2=BD•BC,AC2=BC•DC,
解:如图(1)所示,由射影定理知AD2=BD•DC,AB2=BD•BC,AC2=BC•DC,∴
| 1 |
| AD2 |
| 1 |
| BD•DC |
=
| BC2 |
| BD•BC•DC•BC |
| BC2 |
| AB2•AC2 |
又BC2=AB2+AC2,
∴
| 1 |
| AD2 |
| AB2+AC2 |
| AB2•AC2 |
| 1 |
| AB2 |
| 1 |
| AC2 |
所以
| 1 |
| AD2 |
| 1 |
| AB2 |
| 1 |
| AC2 |
类比AB⊥AC,AD⊥BC猜想:
四面体A-BCD中,AB、AC、AD两两垂直,
AE⊥平面BCD,则
| 1 |
| AE2 |
| 1 |
| AB2 |
| 1 |
| AC2 |
| 1 |
| AD2 |
如图(2),连接BE交CD于F,
连接AF.∵AB⊥AC,AB⊥AD,
∴AB⊥平面ACD.
而AF?平面ACD,∴AB⊥AF.
在Rt△ABF中,AE⊥BF,
∴
| 1 |
| AE2 |
| 1 |
| AB2 |
| 1 |
| AF2 |
在Rt△ACD中,AF⊥CD,
∴
| 1 |
| AF2 |
| 1 |
| AC2 |
| 1 |
| AD2 |
∴
| 1 |
| AE2 |
| 1 |
| AB2 |
| 1 |
| AC2 |
| 1 |
| AD2 |
点评:本题考查利用类比推理得到结论、证明类比结论时证明过程与其类比对象的证明过程类似或直接转化为类比对象的结论.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
在Rt△ABC中,∠A=90°,|
|=1,则
•
的值为:( )
| AB |
| AB |
| BC |
| A、1 | B、-1 |
| C、1或-1 | D、不能确定 |
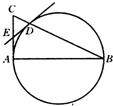 15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.