题目内容
17.已知双曲线Γ:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的离心率为2,过双曲线Γ的左焦点F作圆O:x2+y2=a2的两条切线,切点分别为A、B,则∠AFB=60°.分析 利用双曲线的离心率,结合圆的切线与x轴的关系,推出∠AFB的大小即可.
解答 解:双曲线Γ:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的离心率为2,
可得$\frac{c}{a}$=2,
过双曲线Γ的左焦点F作圆O:x2+y2=a2的两条切线,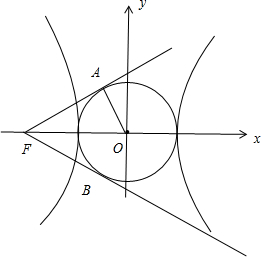
可得sin$(\frac{1}{2}∠AFB)$=$\frac{a}{c}$=$\frac{1}{2}$,
$\frac{1}{2}∠AFB=30°$∴∠AFB=60°.
故答案为:60.
点评 本题考查双曲线的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
2.已知函数f(x)=$\sqrt{{x}^{2}-2x-3}$的定义域为F,g(x)=$\sqrt{\frac{x+1}{x-3}}$的定义域为G,那么集合F,G的关系是( )
| A. | F=G | B. | F⊆G | C. | G⊆F | D. | F∪G=G |
9.一个几何体的三视图如图所示,其中俯视图与侧视图都是半径为2的圆,则这个几何体的体积是( )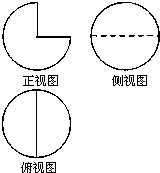

| A. | 8π | B. | 16π | C. | $\frac{8π}{3}$ | D. | $\frac{16π}{3}$ |
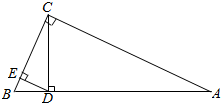 如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥BC于E,若AD=$\frac{3}{2}$$\sqrt{10}$,BE=2.求BC的长.
如图所示,在△ABC中,∠ACB=90°,CD⊥AB于点D,DE⊥BC于E,若AD=$\frac{3}{2}$$\sqrt{10}$,BE=2.求BC的长.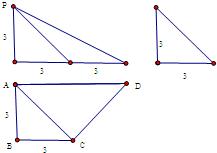 已知四棱锥P-ABCD的三视图如图所示,
已知四棱锥P-ABCD的三视图如图所示,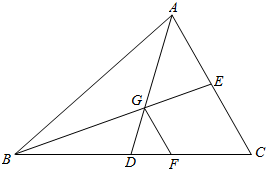
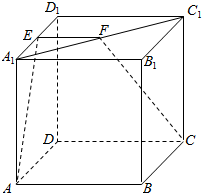 如图,正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点,求:
如图,正方体ABCD-A1B1C1D1中,E、F分别是A1D1、A1C1的中点,求: