题目内容
【题目】已知函数![]() (k为常数,e为自然对数的底数),曲线
(k为常数,e为自然对数的底数),曲线![]() 在点(1, f (1))处的切线与x轴平行.
在点(1, f (1))处的切线与x轴平行.
(1)求k的值;
(2)求![]() 的单调区间;
的单调区间;
(3)设![]() 其中
其中![]() 为
为![]() 的导函数,证明:对任意
的导函数,证明:对任意![]()
【答案】(1)![]() ;(2)
;(2) ![]() 在区间
在区间![]() 内为增函数;在
内为增函数;在![]() 内为减函数;(3)见解析.
内为减函数;(3)见解析.
【解析】分析:(1)由导数的几何意义得![]() ,即可得解;
,即可得解;
(2)求导,导数大于0可得增区间,导数小于0可得减区间;
(3)由![]() ,当
,当![]() ,分析单调性易证得成立;当
,分析单调性易证得成立;当![]() ,分析不等式,只需证
,分析不等式,只需证![]() 即可,设
即可,设![]() ,求导求最值即可证得
,求导求最值即可证得![]() ,
,![]() ,从而得证.
,从而得证.
详解:(1)由f(x) = ![]() 可得
可得![]()
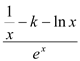 ,而
,而![]() ,
,
即![]() ,解得
,解得![]() ;
;
(2)![]()
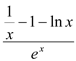 ,令
,令![]() 可得
可得![]() ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 。
。
于是![]() 在区间
在区间![]() 内为增函数;在
内为增函数;在![]() 内为减函数.
内为减函数.
(3)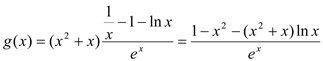 ,
,
当![]() 时,
时, ![]() ,
,![]() .
.
当![]() 时,要证
时,要证 .
.
只需证![]() 即可
即可
设函数![]() .
.
则![]() ,
,
则当![]() 时
时![]() ,
,
令![]() 解得
解得![]() ,
,
当![]() 时
时![]() ;当
;当![]() 时
时![]() ,
,
则当![]() 时
时![]() ,且
,且![]() ,
,
则![]()
![]() ,于是可知当
,于是可知当![]() 时
时![]() 成立
成立
综合(1)(2)可知对任意x>0,![]() 恒成立.
恒成立.
【另证1】设函数![]() ,则
,则![]() ,
,
则当![]() 时
时![]() ,
,
于是当![]() 时,要证
时,要证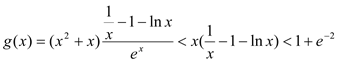 ,
,
只需证![]() 即可,
即可,
设![]() ,
,![]() ,
,
令![]() 解得
解得![]() ,
,
当![]() 时
时![]() ;当
;当![]() 时
时![]() ,
,
则当![]() 时
时![]() ,
,
于是可知当![]() 时
时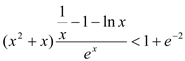 成立
成立
综合(1)(2)可知对任意x>0,![]() 恒成立.
恒成立.
【另证2】根据重要不等式当![]() 时
时![]() ,即
,即![]() ,(要证明)
,(要证明)
于是不等式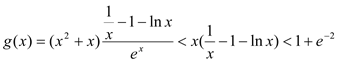 ,
,
设![]() ,
,![]() ,
,
令![]() 解得
解得![]() ,
,
当![]() 时
时![]() ;当
;当![]() 时
时![]() ,
,
则当![]() 时
时![]() ,
,
于是可知当![]() 时
时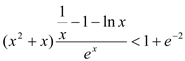 成立.
成立.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目


