题目内容

解:(Ⅰ)当 时,函数
时,函数 ,则
,则 .
.
 得:
得:
当 变化时,
变化时, ,
,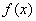 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 极大 |
| 极小 |
|
因此,当 时,
时,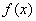 有极大值,并且
有极大值,并且 ;
;
当 时,
时,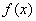 有极小值,并且
有极小值,并且 .--------------------------------4分
.--------------------------------4分
(Ⅱ)由 ,则
,则 ,
,
解 得
得 ;解
;解 得
得
所有 在
在 是减函数,在
是减函数,在 是增函数,
是增函数,
即
对于任意的 ,不等式
,不等式 恒成立,则有
恒成立,则有 即可.
即可.
即不等式 对于任意的
对于任意的 恒成立.--------------------------------6分
恒成立.--------------------------------6分

(1)当 时,
时, ,解
,解 得
得 ;解
;解 得
得 ,
,
所以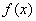 在
在 是增函数,在
是增函数,在 是减函数,
是减函数, ,
,
所以 符合题意.
符合题意.


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目








 中,
中, 分别是角
分别是角 所对的边,且
所对的边,且 .
. ;
; ,求
,求 的取值范围.
的取值范围. 为等差数列,
为等差数列, 是其前
是其前 项和,且
项和,且 ,则
,则 的值为_______.
的值为_______. 在点
在点 处的切线平行于直线
处的切线平行于直线 ,则点
,则点 B.
B. C.
C. D.
D.  中,直线
中,直线 的参数方程为
的参数方程为 ,(
,( 为参数),以坐标原点为极点,
为参数),以坐标原点为极点, 的极坐标方程为
的极坐标方程为
 是曲线
是曲线 的取值范围.
的取值范围. ,
, 则线段AB的中点
则线段AB的中点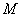 的坐标为 ( )
的坐标为 ( ) B.
B.  C.
C.  D.
D. 
 为正四面体,
为正四面体, 于点
于点 ,点
,点 均在平面
均在平面 外,且在平面
外,且在平面 的中点为
的中点为 ,则直线
,则直线 与平面
与平面 B.
B. C.
C. D.
D.

 ≤1,如果p是q的充分不必要条件,则k的取值范围是
≤1,如果p是q的充分不必要条件,则k的取值范围是 B.
B.  C. (-∞,—1) D.
C. (-∞,—1) D. 