题目内容
已知函数
在[-1，0]上是增函数，则实数a的取值范围是________．
（0，1）
分析：根据复合函数单调性的判定方法，同增异减，和一次函数y=kx+b（k≠0），知当k＞0时，函数f（x）在R上是增函数，当k＜0时，函数f（x）在R上是减函数；由已知函数在[-1，0]上是增函数，讨论a可知y=1-ax在区间[-1，0]上是单调性，从而求出a的范围，注意函数的定义域．
解答：∵函数在[-1，0]上是增函数
当a＞1时，y=1-ax在[-1，0]上是增函数则a＜0，故a不存在
当a＜1时，y=1-ax在[-1，0]上是增函数则a＞0，故0＜a＜1
故答案为：（0，1）
点评：考查简单的复合函数和基本初等函数的单调性，注意掌握反比例函数、一次函数、二次函数、指数函数、对数函数等的单调性，属基础题．
分析：根据复合函数单调性的判定方法，同增异减，和一次函数y=kx+b（k≠0），知当k＞0时，函数f（x）在R上是增函数，当k＜0时，函数f（x）在R上是减函数；由已知函数
在[-1，0]上是增函数，讨论a可知y=1-ax在区间[-1，0]上是单调性，从而求出a的范围，注意函数的定义域．解答：∵函数
在[-1，0]上是增函数当a＞1时，y=1-ax在[-1，0]上是增函数则a＜0，故a不存在
当a＜1时，y=1-ax在[-1，0]上是增函数则a＞0，故0＜a＜1
故答案为：（0，1）
点评：考查简单的复合函数和基本初等函数的单调性，注意掌握反比例函数、一次函数、二次函数、指数函数、对数函数等的单调性，属基础题．
练习册系列答案
相关题目
在[1，＋∞）上为增函数，且θ∈（0，π），
，m∈R．
在[1，＋∞）上为单调函数，求m的取值范围；
，若在[1，e]上至少存在一个
，使得
成立，求
的取值范围．
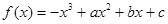在（-∞，0）上是减函数，在（0，1）上是增函数，函数
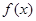在R上有三个零点，且1是其中一个零点。
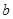的值；（Ⅱ）求
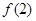的取值范围；
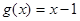，且
的解集为（-∞，1），求实数
的取值范围。
在[-1，0]上是增函数，则实数a的取值范围是 ．
在[-1，0]上是增函数，则实数a的取值范围是 ．