题目内容
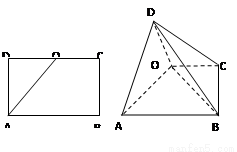
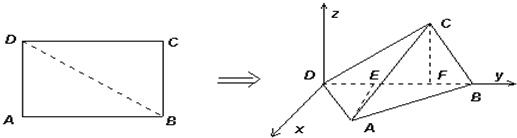
如图,已知矩形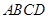 中,
中,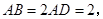
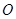 为
为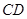 的中点,沿
的中点,沿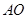 将三角形
将三角形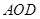 折起,使
折起,使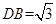 .
.
(Ⅰ)求证:平面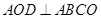 ;
;
(Ⅱ)求直线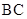 与平面
与平面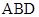 所成角的正弦值.
所成角的正弦值.
【答案】
(Ⅰ)详见解析;(Ⅱ)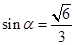 .
.
【解析】
试题分析:(Ⅰ)取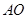 中点H,先证明
中点H,先证明 垂直于平面
垂直于平面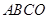 ,进而证明平面
,进而证明平面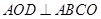 ;(Ⅱ)建立直角坐标系,构造向量
;(Ⅱ)建立直角坐标系,构造向量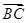 ,平面
,平面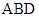 的法向量
的法向量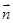 ,利用公式求解.
,利用公式求解.
试题解析:(Ⅰ)∵在矩形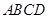 中,
中,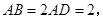
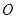 为
为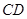 的中点,
的中点,
∴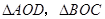 为等腰直角三角形,
为等腰直角三角形,
∴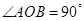 ,即
,即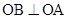 .
(1分)
.
(1分)
取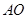 中点H,连结
中点H,连结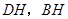 ,则
,则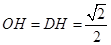 ,
,
在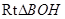 中,
中,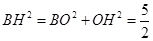 ,
,
在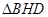 中,
中,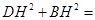
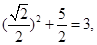 又
又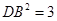 ,
,
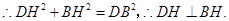 (2分)
(2分)
又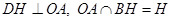 (3分)
(3分)
∴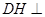 面
面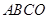 ,
(4分)
,
(4分)
而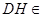 平面
平面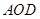 ,
(5分)
,
(5分)
∴平面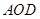 ⊥平面
⊥平面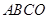 .
(6分)
.
(6分)
(Ⅱ)解:分别以直线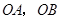 为x轴和y轴,O为坐标原点,建立如图所示的空间直角坐标系,
为x轴和y轴,O为坐标原点,建立如图所示的空间直角坐标系,

则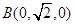 ,
,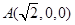 ,
, ,
,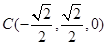 .
.
∴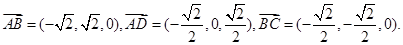 (7分)
(7分)
设平面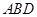 的一个法向量为
的一个法向量为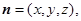
由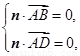 得
得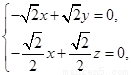
即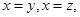 令
令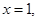 则
则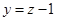 ,
,
取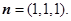 (9分)
(9分)
设 为直线
为直线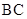 与平面
与平面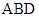 所成的角,
所成的角,
则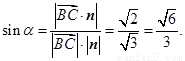 (11分)
(11分)
即直线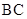 与平面
与平面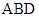 所成角的正弦值为
所成角的正弦值为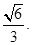 (12分)
(12分)
考点:1.面面垂直的判定;2.线面角的求解;3利用空间直角坐标系求线面角.

练习册系列答案
相关题目
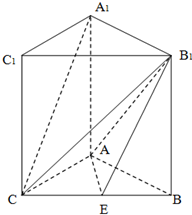 如图,已知矩形AA1B1B中,AA1=2,AB=1,若矩形AA1C1C是矩形AA1B1B绕AA1旋转而成,记二面角B-AA1-C的大小为θ,θ∈(0,π),E是BC的中点.
如图,已知矩形AA1B1B中,AA1=2,AB=1,若矩形AA1C1C是矩形AA1B1B绕AA1旋转而成,记二面角B-AA1-C的大小为θ,θ∈(0,π),E是BC的中点.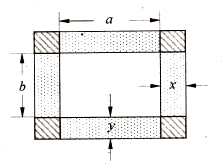 (2012•江苏二模)如图,已知矩形油画的长为a,宽为b.在该矩形油画的四边镶金箔,四个角(图中斜线区域)装饰矩形木雕,制成一幅矩形壁画.设壁画的左右两边金箔的宽为x,上下两边金箔的宽为y,壁画的总面积为S.
(2012•江苏二模)如图,已知矩形油画的长为a,宽为b.在该矩形油画的四边镶金箔,四个角(图中斜线区域)装饰矩形木雕,制成一幅矩形壁画.设壁画的左右两边金箔的宽为x,上下两边金箔的宽为y,壁画的总面积为S. (2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使
(2013•临沂二模)如图,已知矩形ABCD中,AB=2AD=2,O为CD的中点,沿AO将三角形AOD折起,使