题目内容
5．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{c}x+\frac{3}{8}，（0＜x＜c）}\\{{2}^{-8c}，（c≤x＜1）}}\end{array}\right.$，且满足f（$\sqrt{c}$）=$\frac{1}{4}$．（1）求常数c的值；
（2）解不等式f（x）＞$\frac{1}{8}$．
分析 （1）先判断$\sqrt{c}$与c的大小，代值计算即可；
（2）根据x的范围，分段求出，得到不等式的解集．
解答 解：（1）∵0＜c＜1，
∴$\sqrt{c}$＞c，又f（$\sqrt{c}$）=$\frac{1}{4}$，
∴2-8c=$\frac{1}{4}$=2-2，
解得c=$\frac{1}{4}$；
（2）由（1）知，f（x）=$\left\{\begin{array}{l}{\frac{1}{2}x+\frac{3}{8}，0＜x＜\frac{1}{4}}\\{\frac{1}{4}，\frac{1}{4}≤x＜1}\end{array}\right.$，
∵f（x）＞$\frac{1}{8}$，
当0＜x＜$\frac{1}{4}$，$\frac{1}{2}$x+$\frac{3}{8}$＞$\frac{1}{8}$，解得0＜x＜$\frac{1}{4}$，
当$\frac{1}{4}$≤x＜1时，f（x）＞$\frac{1}{8}$恒成立，
综上所述：不等式的解集为（0，1）．
点评 本题考查指数型不等式的解法，考查分类讨论思想与方程思想的综合运用，属于中档题．
练习册系列答案
相关题目
16．以下判断正确的是（ ）
| A． | x＞5是命题 | |
| B． | 命题“存在x∈R，x2+x-1＜0”的否定是“任意x∈R，x2+x-1＞0” | |
| C． | 命题“在△ABC中，若A＞B，则sinA＞sinB”的逆命题为假命题 | |
| D． | “b=0”是“函数f（x）=ax2+bx+c是偶函数”的充要条件 |
20．
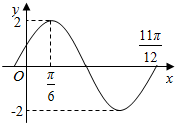已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在一个周期内的图象如图所示，若方程f（x）=m在区间[0，π]上有两个不同的数解x1、x2，则x1+x2的值为（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）在一个周期内的图象如图所示，若方程f（x）=m在区间[0，π]上有两个不同的数解x1、x2，则x1+x2的值为（ ）| A． | $\frac{π}{3}$ | B． | $\frac{2}{3}π$ | C． | $\frac{4}{3}π$ | D． | $\frac{π}{3}$或$\frac{4}{3}π$ |
10．已知点G是△ABC的重心，且AG⊥BG，若λ=$\frac{si{n}^{2}C}{cosCsinAsinB}$，则实数λ的值为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | 3 | D． | 2 |
14．一菱形土地的面积为$\sqrt{3}$平方公里，菱形的最小角为60度，如果要将这一菱形土地向外扩张变成一正方形土地，问正方形土地边长最小为多少公里（ ）
| A． | $\sqrt{2}$ | B． | $\sqrt{3}$ | C． | $\sqrt{6}$ | D． | 2$\sqrt{6}$ |