题目内容

(理)已知函数f(x)=(n∈N*)的最大值为an,最小值为bn.

(1)设数列{an}的前n项和为Sn(n∈N*),求证:.

(2)若数列{dn}满足:d1=6,dn·dn+1=144·(-)n,设Tn=d1d2d3…dn(n∈N*),试问Tn是否存在最大值?若存在,请求出对应的n的值;若不存在,请说明理由.

答案：(理)解:(1)易得f(x)= 的定义域为［0,n］.

令f′(x)=.

所以函数f(x)在(0,)上单调递增,在(,n)上单调递减.

所以an=.

由于≤n,所以bn=.

因为,所以.

(2)令cn=dn·dn+1,所以Tn=d1d2d3…dn=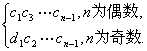

由cn=144·(-)n知|cn|≠1.当|cn|＞1时解得n≤7;当|cn|＜1时解得n≥8.

所以|T2|＜|T4|＜|T6|＜|T8|＞|T10|＞…,|T1|＜|T3|＜|T5|＜|T7|＞…＞|T11|＞….

又dndn+1=144·(-)n,所以dn+1dn+2=144·(-)n+1.相除,得=-,由d1=6得d2=-12,所以d8=＞1.因为|T8|=|T7|·d8,所以T8＞T7＞0,即T8最大,此时n=8.

练习册系列答案
相关题目
精英家教网精英家教网（理）已知函数f(x)=
ln(2-x2)
|x+2|-2
．
（1）试判断f（x）的奇偶性并给予证明；
（2）求证：f（x）在区间（0，1）单调递减；
（3）如图给出的是与函数f（x）相关的一个程序框图，试构造一个公差不为零的等差数列
{an}，使得该程序能正常运行且输出的结果恰好为0．请说明你的理由．
（文）如图，在平面直角坐标系中，方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直，且AC和BD分别在x轴和y轴上．
（1）求证：F＜0；
（2）若四边形ABCD的面积为8，对角线AC的长为2，且
AB
•
AD
=0，求D2+E2-4F的值；
（3）设四边形ABCD的一条边CD的中点为G，OH⊥AB且垂足为H．试用平面解析几何的研究方法判
断点O、G、H是否共线，并说明理由．
（理）已知函数f(x)=
sin2x-(a-4)(sinx-cosx)+a
的定义域为{x|2kπ≤x≤2kπ+
π
2
，k∈Z}，则实数a的取值范围是
 
．
（2011•普陀区三模）（理）已知函数f(x)=
sinπxx∈[0，1]
log2011xx∈(1，+∞)
若满足f（a）=f（b）=f（c），（a、b、c互不相等），则a+b+c的取值范围是
（2，2012）
（2，2012）
．
（2011•普陀区三模）（理）已知函数f(x)=
ln(2-x2)|x+2|-2
．
（1）试判断f（x）的奇偶性并给予证明；
（2）求证：f（x）在区间（0，1）单调递减；
（3）右图给出的是与函数f（x）相关的一个程序框图，试构造一个公差不为零的等差数列{an}，使得该程序能正常运行且输出的结果恰好为0．请说明你的理由．
（2009•嘉定区一模）（理）已知函数f(x)=log2
2
x
1-x
，P1（x1，y1）、P2（x2，y2）是f（x）图象上两点．
（1）若x1+x2=1，求证：y1+y2为定值；
（2）设Tn=f(
1
n
)+f(
2
n
)+…+f(
n-1
n
)，其中n∈N*且n≥2，求Tn关于n的解析式；
（3）对（2）中的Tn，设数列{an}满足a1=2，当n≥2时，an=4Tn+2，问是否存在角a，使不等式(1-
1
a1
)(1-
1
a2
)…(1-
1
an
)＜
sinα
2n+1
对一切n∈N*都成立？若存在，求出角α的取值范围；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网