Question

（2012•贵州模拟）正三棱锥P-ABC中，PA=1，则其体积的最大值是

1

6

．

Answer 1

分析：设H为底面△ABC的中心，延长AH交BC于E，连接PH．设AB=x，则AH=

3

3

x，得三棱锥P-ABC体积V=

1

12

x²

3-x2

，最后利用基本不等式求最值，可得当且仅当x=

2

时，正三棱锥P-ABC体积的最大值为

1

6

．

解答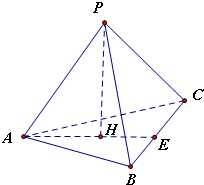：解：设H为底面△ABC的中心，延长AH交BC于E，连接PH
∵三棱锥P-ABC是正三棱锥
∴PH⊥平面ABC，且AE是BC边上的中线
设AB=x，则AH=

2

3

AE=

2

3

•

3

2

x=

3

3

x
Rt△PAH中，PH=

PA2-AH2

=

1- 1 3 x2

∴三棱锥P-ABC体积V=

1

3

S_△ABC•AH=

1

3

×

3

4

x²×

1- 1 3 x2

=

1

12

x²

3-x2

∵x²

3-x2

=2

1 2 x2• 1 2 x2•(3-x2)

，
且

1

2

x2•

1

2

x2•（3-x²）≤（

1 2 x2+ 1 2 x2+(3-x2)

3

）³=1
∴x²

3-x2

≤2，可得V=

1

12

x²

3-x2

≤

1

6

当且仅当

1

2

x2=3-x²时，即x=

2

时，正三棱锥P-ABC体积的最大值为

1

6

故答案为：

1

6

点评：本题给出正三棱锥的侧棱长为1，求体积的最大值．着重考查了正三棱锥的性质和锥体体积公式等知识，属于中档题．