题目内容
已知 是方程
是方程 的一个解,α∈(-π,0),则α= .
的一个解,α∈(-π,0),则α= .
【答案】分析:先将 代入求出tan(-
代入求出tan(- )的值,再由正切函数的性质可得到α的值,最后根据α的范围确定最后答案.
)的值,再由正切函数的性质可得到α的值,最后根据α的范围确定最后答案.
解答:解:将 代入
代入
得3tan(- )=
)= ∴tan(-
∴tan(- )=
)= ∴-
∴- =
=
∴α= ,又∵α∈(-π,0),
,又∵α∈(-π,0),
故答案为:-
点评:本题主要考查正切函数的基本性质.属基础题.
 代入求出tan(-
代入求出tan(- )的值,再由正切函数的性质可得到α的值,最后根据α的范围确定最后答案.
)的值,再由正切函数的性质可得到α的值,最后根据α的范围确定最后答案.解答:解:将
 代入
代入
得3tan(-
 )=
)= ∴tan(-
∴tan(- )=
)= ∴-
∴- =
=
∴α=
 ,又∵α∈(-π,0),
,又∵α∈(-π,0),故答案为:-

点评:本题主要考查正切函数的基本性质.属基础题.

练习册系列答案
相关题目
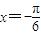 是方程
是方程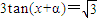 的一个解,α∈(-π,0),则α= .
的一个解,α∈(-π,0),则α= .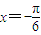 是方程
是方程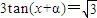 的一个解,α∈(-π,0),则α= .
的一个解,α∈(-π,0),则α= .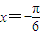 是方程
是方程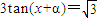 的一个解,α∈(-π,0),则α= .
的一个解,α∈(-π,0),则α= .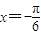 是方程
是方程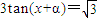 的一个解,α∈(-π,0),则α= .
的一个解,α∈(-π,0),则α= .