题目内容
已知实数a≠b,试解关于x的不等式:(
)b2(x-1)-a2x≥2[ax+b(1-x)]2.
| 1 | 2 |
分析:不等式即2a2x-b2(x-1)≥2[ax+b(1-x)]2,由此可得 a2x-b2(x-1)≥[ac+b(1-x)2]2,化简为 (a-b)2x≥(a-b)2x2,即x≥x2,由此解得x的范围
解答:解:由于实数a≠b,关于x的不等式:(
)b2(x-1)-a2x≥2[ax+b(1-x)]2,即2a2x-b2(x-1)≥2[ax+b(1-x)]2,
∴a2x-b2(x-1)≥[ac+b(1-x)2]2,
∴(a2-b2)x+b2≥a2x2+b2(1-x)2+2abx(1-x),
∴(a-b)2x≥(a-b)2x2,
∴x≥x2,解得 0≤x≤1,
故不等式的解集为[0,1].
| 1 |
| 2 |
∴a2x-b2(x-1)≥[ac+b(1-x)2]2,
∴(a2-b2)x+b2≥a2x2+b2(1-x)2+2abx(1-x),
∴(a-b)2x≥(a-b)2x2,
∴x≥x2,解得 0≤x≤1,
故不等式的解集为[0,1].
点评:本题主要考查复合函数的单调性的应用,指数不等式的解法,属于中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
 。
。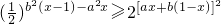 .
. .
.