题目内容
已知函数![]()
![]() 是奇函数.
是奇函数.
(1)求实数m的值;
(2)判断函数![]() 在
在![]() 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当![]() ??
??![]() 时,函数
时,函数![]() 的值域是
的值域是![]() ,求实数
,求实数![]() 与
与![]()
(1)![]()
(2)当![]() 时,
时,![]() 在
在![]() 上是减函数.
上是减函数.
当![]() 时,
时,![]() 在
在![]() 上是增函数.
上是增函数.
(3)![]() ,
,![]()
解析:
(1)由已知条件得![]() 对定义域中的
对定义域中的![]() 均成立.………………2分
均成立.………………2分
![]()
![]() 即
即![]() ………4分
………4分
![]()
![]() 对定义域中的
对定义域中的![]() 均成立.
均成立.![]()
![]() 即
即![]() (舍去)或
(舍去)或![]() .…6分
.…6分
(2)由(1)得![]() ,设
,设![]()
∴ 当![]() 时,
时,![]() ∴
∴ ![]() .………8分
.………8分
当![]() 时,
时,![]() ,即
,即![]() .……………………………………9分
.……………………………………9分
∴ 当![]() 时,
时,![]() 在
在![]() 上是减函数. ………………………………………10分
上是减函数. ………………………………………10分
同理当![]() 时,
时,![]() 在
在![]() 上是增函数. …………………………………11分
上是增函数. …………………………………11分
(3)∵ ![]() ??
??![]() , ∴ 1≤n<a-2 …………12分
, ∴ 1≤n<a-2 …………12分
∴ a>3 ∴ ![]() 在
在![]() 为减函数 …………13分
为减函数 …………13分
要使![]() 的值域为
的值域为![]() , 则
, 则 ……15分
……15分
∴ ![]() ,
,![]() .………16分
.………16分

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
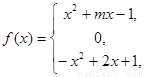
 是奇函数.
是奇函数.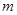 的值;
的值; 在区间
在区间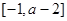 上单调递增,求实数
上单调递增,求实数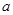 的取值范围;
的取值范围;
 是奇函数.
是奇函数.