Question

已知函数f（x）=a^x（a＞0，且a≠1），根据图象判断［f（x₁）+f（x₂）］与f（）的大小，并加以证明.

Answer 1

解析：对a＞1及0＜a＜1两种情形的指数函数图象，分别取两点A（x₁，f（x₁））、B（x₂，f（x₂））连线段，其中［f（x₁）+f（x₂）］就是这线段中点M的函数值，f（）就是图象上弧线段与直线x=的交点M的函数值，如下图.

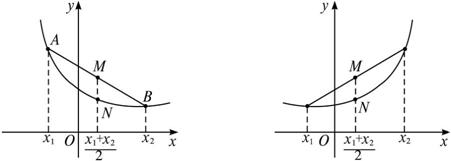
    显然无论哪一种情形总有点N在点M下方.

∴f（）＜［f（x₁）+f（x₂）］.

证明：f（x₁）+f（x₂）-2f（）=.

    由x₁≠x₂，∴≠.∴≠0，∴＞0.

∴f（x₁）+f（x₂）-2f（）＞0.