题目内容
定义在(-∞,+∞)上的偶函数f(x)满足f(x+1)=-f(x),且在[-1,0]上是增函数,下面是关于f(x)的判断:
①f(x)是周期函数;
②f(x)的图象关于点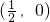 中心对称;
中心对称;
③f(x)的图象关于直线x=1对称;
④f(x)在[0,1]上是增函数;
其中正确的判断是________(把所有正确的判断都填上).
①②③
分析:由f(x+1)=-f(x)可得f(x+2)=f(x),即可得周期T,可判断①
由f(-x)=f(x),f(x+1)=-f(x)可得f(1+x)=-f(-x),则可求f(x)图象关对称中心,又f(x)图象关于y轴(x=0)对称,故x=1也是图象的一条对称轴,故可判断②③
由f(x)为偶函数且在[-1,0]上单增可得f(x)在[0,1]上的单调性,可判断④
解答:由f(x+1)=-f(x)可得f(x+2)=-f(x+1)=-[-f(x)]=f(x),即可得周期T=2,故①正确
由f(x)为偶函数可得f(-x)=f(x),由f(x+1)=-f(x)可得f(1+x)=-f(-x),则f(x)图象关于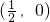 对称,又f(x)图象关于y轴(x=0)对称,故x=1也是图象的一条对称轴,故②③正确;
对称,又f(x)图象关于y轴(x=0)对称,故x=1也是图象的一条对称轴,故②③正确;
由f(x)为偶函数且在[-1,0]上单增可得f(x)在[0,1]上是减函数,故④错
故答案为:①②③
点评:本题考查函数的周期性,函数的单调性及单调区间,函数奇偶性的应用,考查学生分析问题解决问题的能力,是基础题.
分析:由f(x+1)=-f(x)可得f(x+2)=f(x),即可得周期T,可判断①
由f(-x)=f(x),f(x+1)=-f(x)可得f(1+x)=-f(-x),则可求f(x)图象关对称中心,又f(x)图象关于y轴(x=0)对称,故x=1也是图象的一条对称轴,故可判断②③
由f(x)为偶函数且在[-1,0]上单增可得f(x)在[0,1]上的单调性,可判断④
解答:由f(x+1)=-f(x)可得f(x+2)=-f(x+1)=-[-f(x)]=f(x),即可得周期T=2,故①正确
由f(x)为偶函数可得f(-x)=f(x),由f(x+1)=-f(x)可得f(1+x)=-f(-x),则f(x)图象关于
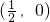 对称,又f(x)图象关于y轴(x=0)对称,故x=1也是图象的一条对称轴,故②③正确;
对称,又f(x)图象关于y轴(x=0)对称,故x=1也是图象的一条对称轴,故②③正确;由f(x)为偶函数且在[-1,0]上单增可得f(x)在[0,1]上是减函数,故④错
故答案为:①②③
点评:本题考查函数的周期性,函数的单调性及单调区间,函数奇偶性的应用,考查学生分析问题解决问题的能力,是基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
已知函数f(x)是定义在R上的奇函数,其最小正周期为3,且x∈(-
,0)时,f(x)=2-x+1则f(8)=( )
| 3 |
| 2 |
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|