Question

【题目】如图，在三棱锥中，平面，，、、分别是棱、、的中点，，．

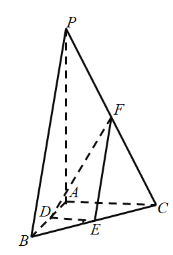
（1）求异面直线与所成的角；

（2）求点到平面的距离．

Answer 1

【答案】(1) (2)

【解析】

（1）由、分别是棱、的中点. 所以，所以(或其补角)为异面直线与所成的角，在中求解.
（2）由是棱的中点，所以点到平面的距离等于点到平面的距离.设点到平面的距离为,由等体积法求解点到平面的距离.

（1）由平面，所以，则

由、分别是棱、的中点. 所以，且

所以(或其补角)为异面直线与所成的角.

由平面，则,又，即.

又,所以平面,

由、分别是棱、的中点. 所以,且

所以平面,则,即.

所以在直角三角形中，.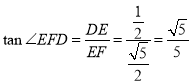

所以异面直线与所成的角为；

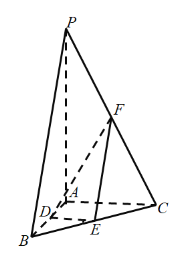
（2）由是棱的中点，所以点到平面的距离等于点到平面的距离.

设点到平面的距离为.

由(1)可知为直角三角形，则.

.

由是棱的中点，所以点到面的距离为

由,所以

所以

所以点到平面的距离为．