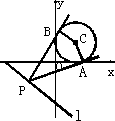题目内容
已知点P是直线l:ax+y=1上任意一点,直线l垂直于直线y=-x+m,EF是圆M:x2+(y-2)2=1的直径,则 的最小值为________.
的最小值为________.
-
分析:数形结合,由 =2
=2 ,平方可得
,平方可得  =
= ,△PEF中,由余弦定理可得 PE2+PF2=2
,△PEF中,由余弦定理可得 PE2+PF2=2  +4,综合可得
+4,综合可得  =PM2-1,由于PM的最小值是点M到直线l:x-y+1=0 的距离,为
=PM2-1,由于PM的最小值是点M到直线l:x-y+1=0 的距离,为  =
= ,由此求得
,由此求得  的最小值.
的最小值.
解答: 解:由两条直线垂直的性质可得-a×(-1)=-1,解得a=-1,
解:由两条直线垂直的性质可得-a×(-1)=-1,解得a=-1,
故直线l:ax+y=1,即 y=x+1.
如图所示:由题意可得M(0,2),EF=2 为直径.
由于 =2
=2 ,平方可得
,平方可得  +
+ +2
+2 =4
=4 ,
,
∴ =
= =
= ①.
①.
△PEF中,由余弦定理可得 EF2=4=PE2+PF2-2PE•PFcos∠EPF
=PE2+PF2-2 ,
,
∴PE2+PF2=2 +4 ②,
+4 ②,
把②代入①可得 =
= =2PM2-
=2PM2- -2,
-2,
∴2 =2 PM2-2,即
=2 PM2-2,即  =PM2-1,故当PM最小时,
=PM2-1,故当PM最小时, 取得最小值.
取得最小值.
由于PM的最小值是点M到直线l:x-y+1=0 的距离,为 =
= ,
,
故 的最小值为 PM2-1=
的最小值为 PM2-1= -1=-
-1=- .
.
故答案为- .
.
点评:本题主要考查两个向量的数量积的运算,直线和圆相交的性质,余弦定理的应用,属于中档题.

分析:数形结合,由
 =2
=2 ,平方可得
,平方可得  =
= ,△PEF中,由余弦定理可得 PE2+PF2=2
,△PEF中,由余弦定理可得 PE2+PF2=2  +4,综合可得
+4,综合可得  =PM2-1,由于PM的最小值是点M到直线l:x-y+1=0 的距离,为
=PM2-1,由于PM的最小值是点M到直线l:x-y+1=0 的距离,为  =
= ,由此求得
,由此求得  的最小值.
的最小值.解答:
 解:由两条直线垂直的性质可得-a×(-1)=-1,解得a=-1,
解:由两条直线垂直的性质可得-a×(-1)=-1,解得a=-1,故直线l:ax+y=1,即 y=x+1.
如图所示:由题意可得M(0,2),EF=2 为直径.
由于
 =2
=2 ,平方可得
,平方可得  +
+ +2
+2 =4
=4 ,
,∴
 =
= =
= ①.
①.△PEF中,由余弦定理可得 EF2=4=PE2+PF2-2PE•PFcos∠EPF
=PE2+PF2-2
 ,
,∴PE2+PF2=2
 +4 ②,
+4 ②,把②代入①可得
 =
= =2PM2-
=2PM2- -2,
-2,∴2
 =2 PM2-2,即
=2 PM2-2,即  =PM2-1,故当PM最小时,
=PM2-1,故当PM最小时, 取得最小值.
取得最小值.由于PM的最小值是点M到直线l:x-y+1=0 的距离,为
 =
= ,
,故
 的最小值为 PM2-1=
的最小值为 PM2-1= -1=-
-1=- .
.故答案为-
 .
.点评:本题主要考查两个向量的数量积的运算,直线和圆相交的性质,余弦定理的应用,属于中档题.

练习册系列答案
相关题目
 已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M
已知抛物线C1:x2=y,圆C2:x2+(y-4)2=1的圆心为点M