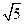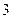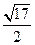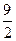题目内容
过椭圆左焦点 且倾斜角为
且倾斜角为 的直线交椭圆于
的直线交椭圆于 两点,若
两点,若 ,则椭圆的离心率等于
,则椭圆的离心率等于
A. | B. | C. | D. |
B
解析考点:椭圆的简单性质.
分析:首先作准线与x轴交点为M,过B准线的垂线,垂足分别为D、C,过B作BH⊥AD,垂足为H,交x轴于E;再设|AB|=5t,易得|BF|=2t,|AF|=3t,结合直线的斜率,可得|AH|=  t,再根据图象,将|AH|用|AF|和|BF|表示,计算可得答案.
t,再根据图象,将|AH|用|AF|和|BF|表示,计算可得答案.
解:作准线与x轴交点为M,过B准线的垂线,垂足分别为D、C,过B作BH⊥AD,垂足为H,交x轴于E.
设|AB|=5t,因为|FA|= |FB|,则|BF|=2t,|AF|=3t,
|FB|,则|BF|=2t,|AF|=3t,
因为AB倾斜角为60°,所以∠ABH=30°,则|AH|= |AB|=
|AB|= t,
t,
|AH|= t-
t- t=
t= t=
t= t,
t,
所以e= ,
,
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知两定点F1(-1,0)、F2(1,0),且|F1F2|是|PF1|与|PF2|的等差中项,则动点P的轨迹是( )
| A.椭圆 | B.双曲线 | C.抛物线 | D.线段 |
.在 中,已知
中,已知 ,且
,且

 ,则
,则 的轨迹方程是( )
的轨迹方程是( )
A. | B. | C. | D. |
已知点A为双曲线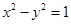 的左顶点,点B和点C在双曲线的右支上,
的左顶点,点B和点C在双曲线的右支上,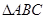 是等边三角形,则
是等边三角形,则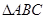 的面积是 ( )
的面积是 ( )
A.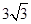 | B.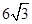 | C.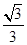 | D. |
若椭圆 的离心率是
的离心率是 则双曲线
则双曲线 的离心率是()
的离心率是()
A. | B. | C. | D. |
已知P是椭圆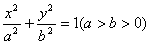 上一点,F1、F2为椭圆两焦点,若∠F1PF2=90°,则ΔF1PF2的面积等于( )
上一点,F1、F2为椭圆两焦点,若∠F1PF2=90°,则ΔF1PF2的面积等于( )
| A.a2 | B.b2 | C.c2 | D.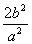 |
已知椭圆 上的一点
上的一点 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为 ,则
,则 到另一焦点距离
到另一焦点距离
| A.2 | B.3 | C.5 | D.7 |
 与直线
与直线 交于A、B两点,满足条件
交于A、B两点,满足条件 的点C也在双曲线上
的点C也在双曲线上 ,则点C的个数为( )
,则点C的个数为( )  个 B.
个 B. 个 C.
个 C.  个
个  D
D .
.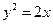 上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为( ).
上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为( ).