Question

已知函数f（x）=|2x-1|+|x+2|+2x（x∈R），
（1）求函数f（x）的最小值；
（2）已知m∈R，命题p：关于x的不等式f（x）≥m²+2m-2对任意x∈R恒成立；命题q：不等式|x-1|+|x-m|＞1  对任意x∈R恒成立．若“p或q”为真，“p且q”为假，求实数m的取值范围．

Answer 1

分析：（1）化简函数f（x）的解析式，作出函数的图象，数形结合，求得函数的最小值．
（2）解一元二次不等式求得命题p，根据函数的恒成立问题化简命题q，求得m的范围，再根据这两个命题一真一假，求得m的范围．

解答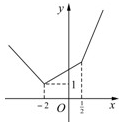：解：（1）由函数f（x）=|2x-1|+|x+2|+2x可得
f（x）=

-x-1  ， x＜-2 x+3  ，  -2≤x≤ 1 2 5x+1  ， x＞ 1 2

，作函数f（x）的图象，
由图可知f（x）在x=-2 处有最小值1．
（2）由（1）知：1≥m²+2m-2，解得-3≤m≤1，所以命题 p：-3≤m≤1．
对于命题q：不等式|x-1|+|x-m|＞1 对任意x∈R恒成立，|x-1|+|x-m|＞|（x-1）-（x-m）|=|m-1|
∴|m-1|＞1，即 m∈（-∞，0）∪（ 2，+∞）．
而“p或q”为真，“p且q”为假，可知命题p与命题q一真一假．
若“p真q假”时，则

-3≤m≤1 0≤m≤2

，解得 0≤m≤1．
若“p假 q真”时，则

m＜-3，或m＞1 m＜0，或m＞2

，解得m＜-3，或 m＞2．
故实数m的取值范围是（-∞，-3）∪[0，1]∪（2，+∞）．

点评：本题主要考查复合命题的真假，带有绝对值的函数，函数的恒成立问题，体现了分类讨论、数形结合的数学思想，属于中档题．