题目内容
下列结论中不正确的是
- A.a>0时,a+
 ≥2
≥2 - B.
 +
+ ≥2
≥2 - C.a2+b2≥2ab
- D.a2+b2≥
B
分析:逐个验证:A由基本不等式可知正确;CD由作差法比较两式的大小可证,B不符合基本不等式的应用条件,并且可举出反例,故错误.
解答:选项A,当a>0时,由基本不等式可得a+ ≥2,当且仅当a=1时取等号,故正确;
≥2,当且仅当a=1时取等号,故正确;
选项B,需在a、b同号时,才有此结论,若a、b异号,可得 ,故错误;
,故错误;
选项C,由a2+b2-2ab=(a-b)2≥0,可得a2+b2≥2ab,当且仅当ab相等时取等号,故正确;
选项D,因为 =
= ,
,
所以 ,也是当且仅当ab相等时取等号,故正确.
,也是当且仅当ab相等时取等号,故正确.
综上可知,只有B错误.
故选B
点评:本题要求选出错误的选项,涉及基本不等式和作差法比较两式的大小,属基础题.
分析:逐个验证:A由基本不等式可知正确;CD由作差法比较两式的大小可证,B不符合基本不等式的应用条件,并且可举出反例,故错误.
解答:选项A,当a>0时,由基本不等式可得a+
 ≥2,当且仅当a=1时取等号,故正确;
≥2,当且仅当a=1时取等号,故正确;选项B,需在a、b同号时,才有此结论,若a、b异号,可得
 ,故错误;
,故错误;选项C,由a2+b2-2ab=(a-b)2≥0,可得a2+b2≥2ab,当且仅当ab相等时取等号,故正确;
选项D,因为
 =
= ,
,所以
 ,也是当且仅当ab相等时取等号,故正确.
,也是当且仅当ab相等时取等号,故正确.综上可知,只有B错误.
故选B
点评:本题要求选出错误的选项,涉及基本不等式和作差法比较两式的大小,属基础题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
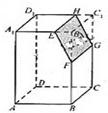 3、如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( )
3、如图,若Ω是长方体ABCD-A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确的是( ) 8、如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
8、如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )