题目内容
已知曲线C :
: (t为参数), C
(t为参数), C :
: (
( 为参数)。
为参数)。
(Ⅰ)化C ,C
,C 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(II)若C 上的点P对应的参数为
上的点P对应的参数为 ,Q为C
,Q为C 上的动点,求
上的动点,求 中点
中点 到直线
到直线
 (t为参数)距离的最大值。
(t为参数)距离的最大值。
【答案】
(I) ,
,
 为圆心是
为圆心是 ,半径是1的圆。
,半径是1的圆。
 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在 轴上,长半轴长是2,短半轴长是4的椭圆。
轴上,长半轴长是2,短半轴长是4的椭圆。
(Ⅱ) 。
。
【解析】本试题主要是考查了参数方程与普通方程的转化以及点到直线的距离公式的求解的综合运用。
(1)消去参数得到普通方程。
(2)因为当 时,
时, ,故
,故
 为直线
为直线 ,
,
那么利用点到直线的距离公式得到。
解:(I) ………………4分
………………4分
 为圆心是
为圆心是 ,半径是1的圆。
,半径是1的圆。
 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在 轴上,长半轴长是2,短半轴长是4的椭圆。
轴上,长半轴长是2,短半轴长是4的椭圆。
……………………………………………………………………6分
(Ⅱ)当 时,
时, ,故
,故
……………………………………………………………8分
 为直线
为直线 ,
,
 到
到 的距离
的距离 ……10分
……10分
从而当 时,
时,
 取得最大值
取得最大值 …………………………………………………12分
…………………………………………………12分

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 :
: (t为参数), C
(t为参数), C :
: (
( 为参数)。
为参数)。 ,Q为C
,Q为C 中点
中点 到直线
到直线 (t为参数)距离的最小值。
(t为参数)距离的最小值。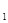 :
: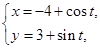 (t为参数), C
(t为参数), C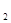 :
: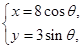 (
(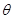 为参数)。
为参数)。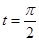 ,Q为C
,Q为C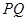 中点
中点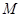 到直线
到直线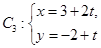 (t为参数)距离的最小值。
(t为参数)距离的最小值。 :
: (t为参数), C
(t为参数), C :
: (
( 为参数)。
为参数)。 ,Q为C
,Q为C 中点
中点 到
到 (t为参数)距离的最小值。
(t为参数)距离的最小值。