题目内容
若函数f(x)=ax2+2x+5在(2,+∞)上是单调递减的,则a的取值范围是______________.
a≤-![]()
解析:若a=0,则f(x)=2x+5,与已知矛盾,∴a≠0.
这时,f(x)=ax2+2x+5=a(x+![]() )2+5-
)2+5-![]() ,对称轴为x=-
,对称轴为x=-![]() ,由题设知
,由题设知![]()
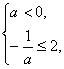 ,解得a≤-
,解得a≤-![]() .
.

练习册系列答案
相关题目
题目内容
若函数f(x)=ax2+2x+5在(2,+∞)上是单调递减的,则a的取值范围是______________.
a≤-![]()
解析:若a=0,则f(x)=2x+5,与已知矛盾,∴a≠0.
这时,f(x)=ax2+2x+5=a(x+![]() )2+5-
)2+5-![]() ,对称轴为x=-
,对称轴为x=-![]() ,由题设知
,由题设知![]()
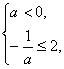 ,解得a≤-
,解得a≤-![]() .
.
