题目内容
若直线
上不同的三个点
与直线外一点
，使得
成立，则满足条件的实数
的集合为（ ）
A． | B． | C． | D． |
D.
解析试题分析：由可得，
=
，由共线知，
，解得
=-1或=0（舍），故选D.
考点：1.向量的运算；2.三点共线的充要条件.
练习册系列答案
相关题目
若平面向量
与向量
平行，且
，则=（）
A． | B． | C． | D．或 |
设O在△ABC内部，且
，则△ABC的面积与△AOC的面积之比为( )
| A．3:1 |
| B．4:1 |
| C．5:1 |
| D．6:1 |
已知O, A, M,B为平面上四点，且
，实数
，则
| A．点M在线段AB上 | B．点B在线段AM上 |
| C．点A在线段BM上 | D．O,A,M,B一定共线 |
设
是非零向量,则
是
的( )
| A．充分不必要条件 | B．必要不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
已知向量a＝(1－t，t)，b＝(2,3)，则|a－b|的最小值为( )
A． | B．2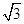 | C．2 | D．4 |
连掷两次骰子得到的点数分别为m和n，记向量
与向量
的夹角为θ，则
的概率是（ ）
A． | B． | C． | D． |
如图,在底面为平行四边形的四棱柱ABCD - A1B1C1D1中,M是AC与BD的交点,若
=a,
=b,
=c,则下列向量中与
相等的向量是( )
A．- a+b+c | B．a+b+c | C．a-b+c | D．-a-b+c |
在四边形ABCD中，
＝(1,2)，
＝(－4,2)，则该四边形的面积为( )
A． | B．2 | C．5 | D．10 |