题目内容
在△ABC中，角A、B、C的对边分别为a、b、c，若
（1）判断△ABC的形状
（2）若
，求cosA的值．
解：（1）∵
（2分）
∴bccosA=accosB∴sinBcosA=sinAcosB（4分）
即sinAcosB-sinBcosA=0∴sin（A-B）=0
∵-π＜A-B＜π∴A=B∴为等腰三角形．（6分）
（2）由（1）知A=B，则：C=π-2A
∴
（8分）
∴
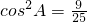（10分）
又因为2A=A+B＜π，得
∴
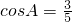（12分）
分析：（1）通过数量积转化为三角恒等式，利用正弦定理推出A=B，得到结论．
（2）利用A=B，则：C=π-2A，通过，求出A的余弦值即可．
点评：本题是基础题，考查向量在三角函数中的应用，解三角形问题，正弦定理的应用，考查计算能力．
（2分）∴bccosA=accosB∴sinBcosA=sinAcosB（4分）
即sinAcosB-sinBcosA=0∴sin（A-B）=0
∵-π＜A-B＜π∴A=B∴为等腰三角形．（6分）
（2）由（1）知A=B，则：C=π-2A
∴
（8分）∴
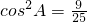（10分）又因为2A=A+B＜π，得
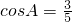∴（12分）分析：（1）通过数量积转化为三角恒等式，利用正弦定理推出A=B，得到结论．
（2）利用A=B，则：C=π-2A，通过
，求出A的余弦值即可．点评：本题是基础题，考查向量在三角函数中的应用，解三角形问题，正弦定理的应用，考查计算能力．
练习册系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a，b，c，若b2+c2-a2=
bc，且b=
a，则下列关系一定不成立的是（ ）
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |