题目内容

（2012•济南三模）若双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)与直线y=
3
x无交点，则离心率e的取值范围（　　）
分析：根据题意，双曲线位于一、三象限的渐近线的斜率小于或等于
3
，满足
b
a
≤
3
，由此结合双曲线基本量的平方关系和离心率的公式，化简整理即可得到该双曲线的离心率e的取值范围．
解答：解：∵双曲线
x2
a2
-
y2
b2
=1(a＞0，b＞0)与直线y=
3
x无交点，
∴双曲线的渐近线方程y=±
b
a
x，满足
b
a
≤
3

得b≤
3
a，两边平方得b2≤3a2，即c2-a2≤3a2，
∴c2≤4a2，得
c2
a2
≤4即e2≤4，
∵双曲线的离心率e为大于1的正数
∴1＜e≤2，
故选B
点评：本题给出双曲线与直线y=
3
x无交点，求双曲线离心率e的取值范围，考查了双曲线的标准方程和简单几何性质等知识，属于基础题．
练习册系列答案
相关题目
（2012•济南三模）经市场调查，某旅游城市在过去的一个月内（以30天计），第t天（1≤t≤30，t∈N﹢）的旅游人数f（t） （万人）近似地满足f（t）=4+
1t
，而人均消费g（t）（元）近似地满足g（t）=120-|t-20|．
（1）求该城市的旅游日收益w（t）（万元）与时间t（1≤t≤30，t∈N﹢）的函数关系式；
（2）求该城市旅游日收益的最小值．
（2012•济南三模）某旅游景点预计2013年1月份起前x个月的旅游人数的和p（x）（单位：万人）与x的关系近似地满足p（x）=
1
2
x（x+1）•（39-2x），（x∈N*，且x≤12）．已知第x月的人均消费额q（x）（单位：元）与x的近似关系是q（x）=
35-2x(x∈N*，且1≤x≤6)
160
x
(x∈N*，且7≤x≤12)

（I）写出2013年第x月的旅游人数f（x）（单位：人）与x的函数关系式；
（II）试问2013年第几月旅游消费总额最大，最大月旅游消费总额为多少元？
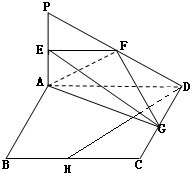（2012•济南三模）如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且2PA=AD，E、F、G、H分别是线段PA、PD、CD、BC的中点．
（Ⅰ）求证：BC∥平面EFG；
（Ⅱ）求证：DH⊥平面AEG；
（Ⅲ）求三棱锥E-AFG与四棱锥P-ABCD的体积比．
（2012•济南三模）已知直线l：y=x+1，圆O：x2+y2=
3
2
，直线l被圆截得的弦长与椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的短轴长相等，椭圆的离心率e=
3
2
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点M（0，-
1
3
）的动直线l交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点T，使得无论l如何转动，以AB为直径的圆恒过定点T？若存在，求出点T的坐标；若不存在，请说明理由．
（2012•济南三模）设函数f（x）=x2-2（-1）klnx（k∈N*），f′（x）表示f（x）导函数．
（I）求函数f（x）的单调递增区间；
（Ⅱ）当k为偶数时，数列{an}满足a1=1，anf′(an)
=a
2
n+1
-3．证明：数列{
a
2
n
}中不存在成等差数列的三项；
（Ⅲ）当k为奇数时，设bn=
1
2
f′(n)-n，数列{bn}的前n项和为Sn，证明不等式(1+bn)
1
bn+1
＞e对一切正整数n均成立，并比较S2012-1与ln2012的大小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网