题目内容
已知等差数列{an}的前n项和为Sn,若S5=5,S10=20,求S15.
解法一:由等差数列前n项和的性质得S5,S10-S5,S15-S10成等差数列,
即2(S10-S5)=S5+(S15-S10),
∴2×(20-5)=5+(S15-20).∴S15=45.
解法二:∵
、
、
成等差数列,
∴2×
=
+
,2×
=
.
∴S15=45.
解法三:由题意知
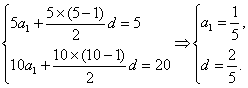
∴S15=15a1+
d=15×
+15×7×
=3+42=45.
练习册系列答案
相关题目
已知等差数列{an}中，a4a6=-4，a2+a8=0，n∈N*．