Question

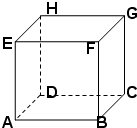设蚂蚁在如图正方体的表面沿棱爬行，它从一个顶点爬向另外三个顶点是等可能的，若蚂蚁的初始位置在顶点A，回答下列问题：
（1）若爬了两条线段（线段可以重复爬行），写出蚂蚁经过的所有路径；
（2）若爬了两条线段（线段可以重复爬行），蚂蚁停在顶点C的概率是多少？
（3）若爬了三条线段（线段可以重复爬行），蚂蚁停在顶点G的概率是多少？

Answer 1

分析：（1）用列举法求得所有路径共9条．
（2）路线如（1）所示，由古典概型得到蚂蚁爬了两条线段停在顶点C的概率．
（3）若爬了三条线段，则蚂蚁所有的爬法共有3³=27种．用列举法求得蚂蚁停在顶点G的爬法有6种，由此求得蚂蚁停在顶点G的概率．

解答：（1）所有路径：A-B-A，A-B-C，A-B-F，A-D-A，A-D-C，A-D-H，
A-E-A，A-E-H，A-E-F，共9条路径．…（2分）
（2）路线如（1）所示，由古典概型得到蚂蚁爬了两条线段停在顶点C的概率为

2

9

． …（3分）
（3）若爬了三条线段，则蚂蚁所有的爬法共有3³=27种．
则蚂蚁停在顶点G的爬法有6种：A-B-C-G，A-B-F-G，A-D-C-G，A-D-H-G，
A-E-F-G，A-E-H-G，
故蚂蚁停在顶点G的概率为

6

27

=

2

9

．…（3分）

点评：本题主要考查等可能事件的概率的求法，体现了分类讨论的数学思想，属于中档题．