题目内容
(本小题满分12分).如图,在直角梯形 中,
中,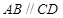 ,
,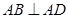 ,且
,且
 ,现以
,现以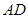 为一边向形外作正方形
为一边向形外作正方形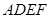 ,然后沿边
,然后沿边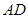 将正方形
将正方形
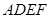 翻折,使平面
翻折,使平面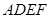 与平面
与平面 垂直,
垂直,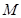 为
为 的中点
的中点
(I) 求证:  ∥平面
∥平面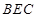 ;
;
(Ⅱ)求证:  平面
平面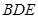 ;
;
(III) 求二面角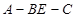 的大小.
的大小.
【答案】
(I)证明:取 中点
中点 ,连结
,连结 .
.
在△ 中,
中, 分别为
分别为 的中点,
的中点,
所以 ∥
∥ ,且
,且 .
.
由已知 ∥
∥ ,
, ,
,
所以 ∥
∥ ,且
,且 .
.
所以四边形 为平行四边形.
为平行四边形.
所以 ∥
∥
又因为 平面
平面 ,且
,且 平面
平面 ,
,
所以 ∥平面
∥平面 .
………………………4分
.
………………………4分
(II)证明:在正方形 中,
中, .
.
又因为平面
 平面
平面 ,且平面
,且平面 平面
平面 ,
,
所以 平面
平面 .
.
所以 .
.
在直角梯形 中,
中, ,
, ,可得
,可得 .
.
在△ 中,
中, ,
所以
,
所以 .
.
所以 .
又
.
又
所以 平面
平面 .
…………………………8分
.
…………………………8分
(III)由已知及(II)得, 两两互相垂直,所以分别以
两两互相垂直,所以分别以 所在直线为
所在直线为 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则

设平面 的法向量为
的法向量为
则由 得
得 取
取 得
得
设平面 的法向量为
的法向量为
则由 得
得 取
取 得
得
 ,
,
所以二面角 的大小为
的大小为 …………………12分
…………………12分
【解析】略

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目