题目内容
(2013•南充三模)已知椭圆的中心在坐标原点,离心率为
,一个焦点是F(0,1).
(Ⅰ)求椭圆方程;
(Ⅱ)直线l过点F交椭圆于A、B两点,且
=2
,求直线l的方程.
| 1 |
| 2 |
(Ⅰ)求椭圆方程;
(Ⅱ)直线l过点F交椭圆于A、B两点,且
| AF |
| FB |
分析:(Ⅰ)设椭圆方程,确定几何量,即可得到椭圆方程;
(Ⅱ)分类讨论,设出直线方程与椭圆方程联立,利用韦达定理及向量条件,即可求得直线方程.
(Ⅱ)分类讨论,设出直线方程与椭圆方程联立,利用韦达定理及向量条件,即可求得直线方程.
解答:解:(Ⅰ)设椭圆方程为
+
=1(a>b>0).
依题意,e=
=
,c=1,∴a=2,b2=a2-c2=3,
∴所求椭圆方程为
+
=1;
(Ⅱ)若直线l的斜率k不存在,则不满足
=2
.
当直线l的斜率k存在时,设直线l的方程为y=kx+1.
因为直线l过椭圆的焦点F(0,1),所以k取任何实数,直线l与椭圆均有两个交点A、B.
设A(x1,y1),B(x2,y2),
联立方程
消去y,得(3k2+4)x2+6kx-9=0.
∴x1+x2=
,①x1•x2=
,②
由F(0,1),A(x1,y1),B(x2,y2),
则
=(-x1,1-y1),
=(x2,y2-1),
∵
=2
,∴(-x1,1-y1)=2(x2,y2-1),得x1=-2x2.
将x1=-2x2代入①、②,得x2=
,③x22=
,④
由③、④得,(
)2=
,化简得
=
,
解得k2=
,∴k=±
∴直线l的方程为:y=±
x+1.
| y2 |
| a2 |
| x2 |
| b2 |
依题意,e=
| c |
| a |
| 1 |
| 2 |
∴所求椭圆方程为
| y2 |
| 4 |
| x2 |
| 3 |
(Ⅱ)若直线l的斜率k不存在,则不满足
| AF |
| FB |
当直线l的斜率k存在时,设直线l的方程为y=kx+1.
因为直线l过椭圆的焦点F(0,1),所以k取任何实数,直线l与椭圆均有两个交点A、B.
设A(x1,y1),B(x2,y2),
联立方程
|
∴x1+x2=
| -6k |
| 3k2+4 |
| -9 |
| 3k2+4 |
由F(0,1),A(x1,y1),B(x2,y2),
则
| AF |
| FB |
∵
| AF |
| FB |
将x1=-2x2代入①、②,得x2=
| 6k |
| 3k2+4 |
| 9 |
| 6k2+8 |
由③、④得,(
| 6k |
| 3k2+4 |
| 9 |
| 6k2+8 |
| 36k2 |
| 3k2+4 |
| 9 |
| 2 |
解得k2=
| 4 |
| 5 |
2
| ||
| 5 |
∴直线l的方程为:y=±
2
| ||
| 5 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 (2013•南充三模)M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
(2013•南充三模)M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.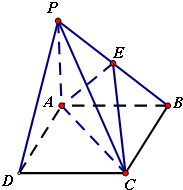 (2013•南充三模)如图,在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4
(2013•南充三模)如图,在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4 (2013•南充三模)如图是一个空间几何体的三视图,这个几何体的体积是( )
(2013•南充三模)如图是一个空间几何体的三视图,这个几何体的体积是( )