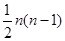题目内容
在古腊毕达哥拉斯学派把1,3,6,10,15,21,28,…这些数叫做三角形数,因为这些数对应的点可以排成一个正三角形如图所示,设第n个三角形数为f(n),则
+
+
…+
=
.
| 1 |
| f(1) |
| 1 |
| f(2) |
| 1 |
| f(3) |
| 1 |
| f(n) |
| 2n |
| n+1 |
| 2n |
| n+1 |

分析:通过观察前几个图形中顶点的个数得,归纳出f(n),然后根据
的特点进行求和.
| 1 |
| f(n) |
解答:解:∵第n个三角形数为f(n),则f(1)=1,f(2)=3,f(3)=6,f(4)=10,f(5)=15,f(6)=21,
第二个图中点的个数比第一个图中点的个数多2,即f(2)-f(1)=2,
第三个图中点的个数比第二个图中点的个数多3,即f(3)-f(2)=3,
第四个图中点的个数比第三个图中点的个数多4,即f(4)-f(3)=4,
…
第n个图中点的个数比第n-1个图中点的个数多n,即f(n)-f(n-1)=n,
等式两边同时相加得:
则f(n)=1+2+3+4+…+n=
,
即
=
=2(
-
).
∴
+
+
…+
=2(1-
+
-
+…+
-
)=2(1-
)=
.
故答案为:
.
第二个图中点的个数比第一个图中点的个数多2,即f(2)-f(1)=2,
第三个图中点的个数比第二个图中点的个数多3,即f(3)-f(2)=3,
第四个图中点的个数比第三个图中点的个数多4,即f(4)-f(3)=4,
…
第n个图中点的个数比第n-1个图中点的个数多n,即f(n)-f(n-1)=n,
等式两边同时相加得:
则f(n)=1+2+3+4+…+n=
| n(n+1) |
| 2 |
即
| 1 |
| f(n) |
| 2 |
| n(n+1) |
| 1 |
| n |
| 1 |
| n+1 |
∴
| 1 |
| f(1) |
| 1 |
| f(2) |
| 1 |
| f(3) |
| 1 |
| f(n) |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
| 2n |
| n+1 |
故答案为:
| 2n |
| n+1 |
点评:本题主要考查归纳推理的应用,根据条件求出f(n),然后求出f(n)的表达式,利用裂项法求和即可.

练习册系列答案
相关题目
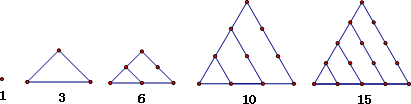

 个三角形数为 (
)
个三角形数为 (
) C.
C.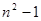 D.
D.