题目内容
已知抛物线y2=2px(p>0),过焦点F的动直线l交抛物线于A、B两点,则我们知道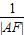 +
+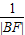 为定值,请写出关于椭圆的类似的结论: ,当椭圆方程为
为定值,请写出关于椭圆的类似的结论: ,当椭圆方程为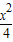 +
+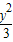 =1时,
=1时,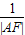 +
+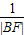 = .
= .
【答案】分析:由类比推理,来得到关于椭圆的类似结论,易知在椭圆中有“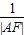 +
+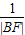 =
=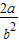 ”求解即可.
”求解即可.
解答:解:已知抛物线y2=2px(p>0),过焦点F的动直线l交抛物线于A、B两点,则我们知道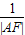 +
+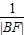 为定值,
为定值,
关于椭圆的类似的结论:过椭圆的焦点F的动直线交椭圆于A、B两点,则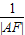 +
+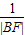 为定值
为定值
已知椭圆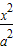 +
+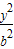 =1(a>b>0),过焦点F的动直线l交椭圆于A、B两点,
=1(a>b>0),过焦点F的动直线l交椭圆于A、B两点,
则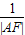 +
+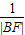 =
=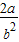 为定值.当椭圆方程为
为定值.当椭圆方程为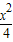 +
+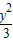 =1时,
=1时,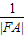 +
+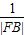 =
= .
.
故答案为:过椭圆的焦点F的动直线交椭圆于A、B两点,则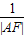 +
+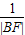 为定值;
为定值;
点评:本题主要考查类比推理,可以先猜测在抛物线中成立的命题在椭圆里面也成立.再计算在这个具体的椭圆里面所求的定值.关于椭圆的一个恒等式:“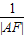 +
+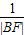 =
=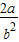 ”是一个经常用到的式子,在以后的学习过程中希望大家多总结.
”是一个经常用到的式子,在以后的学习过程中希望大家多总结.
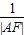 +
+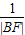 =
=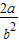 ”求解即可.
”求解即可.解答:解:已知抛物线y2=2px(p>0),过焦点F的动直线l交抛物线于A、B两点,则我们知道
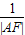 +
+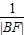 为定值,
为定值,关于椭圆的类似的结论:过椭圆的焦点F的动直线交椭圆于A、B两点,则
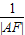 +
+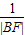 为定值
为定值已知椭圆
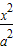 +
+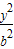 =1(a>b>0),过焦点F的动直线l交椭圆于A、B两点,
=1(a>b>0),过焦点F的动直线l交椭圆于A、B两点,则
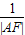 +
+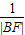 =
=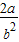 为定值.当椭圆方程为
为定值.当椭圆方程为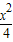 +
+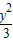 =1时,
=1时,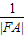 +
+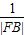 =
= .
.故答案为:过椭圆的焦点F的动直线交椭圆于A、B两点,则
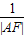 +
+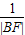 为定值;
为定值;
点评:本题主要考查类比推理,可以先猜测在抛物线中成立的命题在椭圆里面也成立.再计算在这个具体的椭圆里面所求的定值.关于椭圆的一个恒等式:“
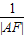 +
+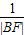 =
=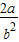 ”是一个经常用到的式子,在以后的学习过程中希望大家多总结.
”是一个经常用到的式子,在以后的学习过程中希望大家多总结. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目