题目内容
给出下列命题
①命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
②命题“存在x0∈R,2x0≤0”的否定是“对任意的x∈R,2x>0”;
③将函数y=|x+1|的图象按向量
=(-1,0)平移,得到的图象的函数表达式为y=|x|;
④将函数y=sinx+1的图象上的所有点的纵坐标变为原来的两倍(横坐标不变),得到的图象的函数表达式为y=2sinx+1.
以上命题正确的是
①命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”;
②命题“存在x0∈R,2x0≤0”的否定是“对任意的x∈R,2x>0”;
③将函数y=|x+1|的图象按向量
| a |
④将函数y=sinx+1的图象上的所有点的纵坐标变为原来的两倍(横坐标不变),得到的图象的函数表达式为y=2sinx+1.
以上命题正确的是
①②
①②
.(注:把你认为正确的命题的序号都填上)分析:本题为多选题,运用所学知识逐一判断,①用否命题的概念判断,命题“若P则q”的否命题为“若¬p则¬q”,只需把条件和结论都加以否定即可,注意大于的否定是小于等于.②用到特称命题的否定是全称命题,③用平移公式计算.④是纵坐标的伸缩变换,将函数y=f(x)的图象上的所有点的纵坐标变为原来的两倍(横坐标不变),得到的图象的函数表达式为y=2f(x).
解答:解:①∵命题“若P则q”的否命题为“若¬p则¬q”,
∴“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”,①正确.
②∵特称命题的否定是全称命题,∴命题“存在x0∈R,2x0≤0”的否定是“对任意的x∈R,2x>0”
∴②正确.
③设函数y=|x+1|的图象上任意一点坐标为(x,y),将函数y=|x+1|的图象按向量
=(-1,0)平移后,点(x,y)对应点为(x′,y′),
∴
,∴
代入(x,y)满足的函数解析式y=|x+1|中,得y′=|x′+2|
∴将函数y=|x+1|的图象按向量
=(-1,0)平移,得到的图象的函数表达式为y=|x+2|,
∴③错误.
④∵将函数y=f(x)的图象上的所有点的纵坐标变为原来的两倍(横坐标不变),得到的图象的函数表达式为y=2f(x).
∴将函数y=sinx+1的图象上的所有点的纵坐标变为原来的两倍(横坐标不变),得到的图象的函数表达式为y=2(sinx+1)=2sinx+2,
∴④错误.
故答案为①②
∴“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”,①正确.
②∵特称命题的否定是全称命题,∴命题“存在x0∈R,2x0≤0”的否定是“对任意的x∈R,2x>0”
∴②正确.
③设函数y=|x+1|的图象上任意一点坐标为(x,y),将函数y=|x+1|的图象按向量
| a |
∴
|
|
代入(x,y)满足的函数解析式y=|x+1|中,得y′=|x′+2|
∴将函数y=|x+1|的图象按向量
| a |
∴③错误.
④∵将函数y=f(x)的图象上的所有点的纵坐标变为原来的两倍(横坐标不变),得到的图象的函数表达式为y=2f(x).
∴将函数y=sinx+1的图象上的所有点的纵坐标变为原来的两倍(横坐标不变),得到的图象的函数表达式为y=2(sinx+1)=2sinx+2,
∴④错误.
故答案为①②
点评:本题综合考查了否命题与原命题的关系,特称命题与全称命题的否定,平移公式,以及函数图象的伸缩变换,考查知识点较多,做题时要细心.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
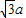 >
>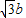 >0”的逆否命题
>0”的逆否命题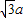 >
>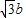 >0”的逆否命题
>0”的逆否命题