题目内容
曲线
在点P(1，12)处的切线与两坐标轴围成三角形的面积是
| A．75 | B． | C．27 | D． |
D
解析试题分析：
点P(1，12)处的切线斜率为3，所以在点P处的切线方程为
即
，令
得
令
得
，所以三角形的面积为
考点：本小题主要考查导数的计算和应用.
点评：求切线方程时，要看清楚求的是在某点处的切线还是过某点的切线.
练习册系列答案
阅读快车系列答案
相关题目
若函数
，
，则函数的极值点的个数是( )
| A．0 | B．1 | C．2 | D．3 |
（ ）
A． | B． | C． | D． |
曲线
在点
处的切线方程为 （ ）
A． | B． |
C． | D． |
是定义在实数集R上的奇函数，且当
时，
成立，若
，
，则
大小关系 （ ）
已知函数
（
为常数）在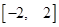
上有最大值3，那么此函数在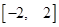上的最小值为（ ）
| A．-29 | B．-37 | C．-5 | D．-1 |
设函数
的导函数为
，且
，则
等于（ ）
A． | B． | C． | D． |
已知一个物体的运动方程是s＝1+t＋t2，其中s的单位是米，t的单位是秒，那么该物体在3秒末的瞬间速度是
| A．6米/秒 | B．7米/秒 | C．8米/秒 | D．9米/秒 |
若
,则
（ ）
A． | B．2 | C． | D． |