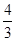题目内容
直线 与圆
与圆 交于A、B两点,O是坐标原点,若直线OA、OB的倾斜面角分别为
交于A、B两点,O是坐标原点,若直线OA、OB的倾斜面角分别为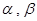 ,则
,则 ( )
( )
A. | B. | C. | D. |
B
解析试题分析:直线 与圆
与圆 交于A、B两点,O是坐标原点,若直线OA、OB的倾斜面角分别为
交于A、B两点,O是坐标原点,若直线OA、OB的倾斜面角分别为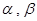 ,而由于圆心(0,0)到直线
,而由于圆心(0,0)到直线 的距离为
的距离为 ,半径为3,那么可知半弦长为
,半径为3,那么可知半弦长为 ,然后借助于勾股定理满足的三角形可知
,然后借助于勾股定理满足的三角形可知
 ,故选B.
,故选B.
考点:直线与圆的位置关系
点评:解决的关键是利用倾斜角和直线与圆相交的性质得到函数值,属于基础题。

练习册系列答案
相关题目
直线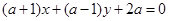 (
(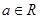 )与圆
)与圆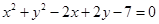 的位置关系是( )
的位置关系是( )
| A.相切 | B.相离 | C.相交 | D.不确定 |
直线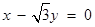 截圆
截圆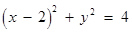 所得劣弧所对的圆心角是
所得劣弧所对的圆心角是
A.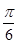 | B.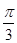 | C.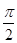 | D.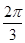 |
以点(-5,4)为圆心,且与 轴相切的圆的方程是( )
轴相切的圆的方程是( )
A. | B. |
C.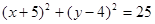 | D. |
已知点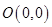 ,
,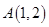 ,
,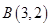 ,以线段
,以线段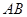 为直径作圆
为直径作圆 ,则直线
,则直线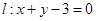 与圆
与圆 的位置关系是
的位置关系是
| A.相交且过圆心 | B.相交但不过圆心 | C.相切 | D.相离 |
直线过点P(0,2),且截圆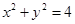 所得的弦长为2,则直线的斜率为
所得的弦长为2,则直线的斜率为
A.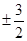 | B.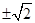 | C.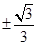 | D.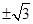 |
已知圆 ,直线
,直线 ,则圆C内任意一点到直线的距离小于
,则圆C内任意一点到直线的距离小于 的概率为( )
的概率为( )
A. | B. | C. | D.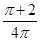 |
圆 上的点到直线
上的点到直线 的距离最大值是( )
的距离最大值是( )
| A.2 | B. | C. | D. |
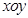 中,圆
中,圆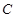 的方程为
的方程为 ,若直线
,若直线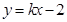 上至少存在一点,使得以该点为圆心,
上至少存在一点,使得以该点为圆心,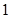 为半径的圆与圆
为半径的圆与圆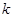 的最大值为
的最大值为