Question

5．正四面体S-ABC中，D为SC的中点，则BD与SA所成角的余弦值是$\frac{\sqrt{3}}{6}$．

Answer 1

分析 由题意画出图象再取AC的中点E，连接DE，BE，则可证得∠BDE就是BD与SA所成的角，在三角形BDE中利用余弦定理求解即可．

解答 解：如图取AC的中点E，连接DE、BE，则DE∥SA，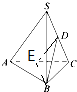
∴∠BDE就是BD与SA所成的角．
设SA=a，则BD=BE=$\frac{\sqrt{3}}{2}a$，DE=$\frac{1}{2}a$，
在△中，cos∠BDE=$\frac{B{D}^{2}+D{E}^{2}-B{E}^{2}}{2BD•DE}$
=$\frac{\frac{1}{4}{a}^{2}}{2×\frac{\sqrt{3}}{2}a×\frac{1}{2}a}$=$\frac{\sqrt{3}}{6}$，
∴BD与SA所成角的余弦值$\frac{\sqrt{3}}{6}$．
故答案为：$\frac{\sqrt{3}}{6}$．

点评 本题考查异面直线及其所成的角，关键是找角，考查了余弦定理的应用，是中档题．