题目内容
已知偶函数f(x)在区间[0,+∞)单调递增,则满足f(2x-1)<f 的x取值范围是 ( )
的x取值范围是 ( )
A. | B. | C. | D. |
A
解析试题分析:根据题意,由于偶函数f(x)在区间[0,+∞)单调递增,那么可知在对称区间x<0上单调递减,同时利用偶函数的对称性可知,要使得f(2x-1)<f ,只要||2x-1|<
,只要||2x-1|<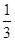 ,解得x取值范围是
,解得x取值范围是 故选A
故选A
考点:抽象函数的性质
点评:本题给出抽象函数为偶函数且在[0,+∞)上为增函数,求关于x的不等式的解集,着重考查了函数单调性的奇偶性等知识,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知函数 下列命题正确的是 ( )
下列命题正确的是 ( )
A.若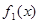 是增函数, 是增函数, 是减函数,则 是减函数,则 存在最大值 存在最大值 |
B.若 存在最大值,则 存在最大值,则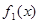 是增函数, 是增函数, 是减函数 是减函数 |
C.若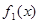 , , 均为减函数,则 均为减函数,则 是减函数 是减函数 |
D.若 是减函数,则 是减函数,则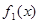 , , 均为减函数 均为减函数 |
若方程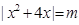 有实数根,则所有实数根的和可能为
有实数根,则所有实数根的和可能为
| A.-2,-4,-6 | B.-4,-5,-6 | C.-3,-4,-5 | D.-4,-6,-8 |
不等式2x2-x-1>0的解集是
A. | B.(1, + ) ) |
C.(- ,1)∪(2,+ ,1)∪(2,+ ) ) | D. |
二次函数f(x)的二次项系数为正数,且对任意xÎR都有f(x)=f(4-x)成立,
若f(2-a2)<f(1+a-a2),那么a的取值范围是 ( )
| A.1<a<2 | B.a>1 | C.a>2 | D.a<1 |
关于x、y的方程组 的解是
的解是 ,则m-n的值是
,则m-n的值是
| A.1 | B.-1 | C.2 | D.不确定 |
碳 的半衰期为5730年,那么碳
的半衰期为5730年,那么碳 的年衰变率为( )
的年衰变率为( )
A. | B. | C. | D. |
函数 的单调减区间为 ( )
的单调减区间为 ( )
A. | B.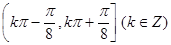 |
C. | D. |
 是以
是以 为周期的偶函数,当
为周期的偶函数,当 时,
时, .若关于
.若关于 的方程
的方程 (
( )在区间
)在区间 内有四个不同的实根,则
内有四个不同的实根,则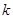 的取值范围是
的取值范围是


