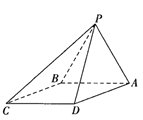
题目内容
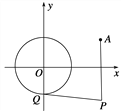
【题目】抛物线
的焦点F为圆C：
的圆心．
求抛物线的方程与其准线方程；
直线l与圆C相切，交抛物线于A，B两点；
若线段AB中点的纵坐标为
，求直线l的方程；
求
的取值范围．
【答案】（1）
,
；（2）
或
；②
【解析】
（1）由圆C：
配方可得：
，可得圆心
可得抛物线的焦点
因此
，解得
，即可得出．
（2）设直线
的方程为：
，
，
由直线与圆
相切，可得：
，或
直线与抛物线联立，化为：
，
进而得到
，或
，根与系数的关系可得
，
，
根据中点坐标公式即可求出m的值，可得直线方程，
利用数量积运算性质，再利用二次函数的单调性即可得出．
解：（1）由圆
配方可得：，可得圆心
．
抛物线的焦点
．
，解得
．
抛物线的准线方程为：．
抛物线的方程为
（2）设直线的方程为：，，
直线与圆相切，
，化为：
．
，或
．
联立
，化为：，
．
，或．
即
，解得
或
所以可得
的范围为或
，．
线段
中点的纵坐标为
，
，
，
，
解得
或
，
故直线的方程为
或
②
.
设
，或
当时，单调递增，
，
当时，单调递减，
．
的取值范围是
．
练习册系列答案
相关题目
【题目】某学校开展主题为“垃圾分类，绿色生活新时尚”的宣传活动，为了解学生对垃圾分类知识的掌握情况，该校环保社团成员在校园内随机抽取了部分学生进行问卷调查，将他们的得分按优秀、良好、合格、待合格四个等级进行统计，并绘制了如下不完整的统计表和条形统计图.请根据以下信息，解答下列问题：
等级 | 频数 | 频率 |
优秀 | 21 | 42% |
良好 |
| 40% |
合格 | 6 |
|
待合格 | 3 | 6% |
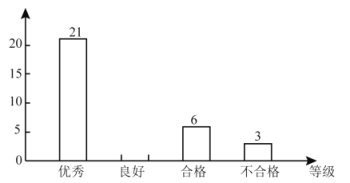
（1）本次调查随机抽取了__________名学生，表中
__________，
__________；
（2）补全条形统计图；
（3）若全校有
名学生，请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.
