题目内容
【题目】若函数
在
处有极值，且
，则称为函数的“F点”.
（1）设函数
（
）.
①当
时，求函数的极值；
②若函数存在“F点”，求k的值；
（2）已知函数
（a，b，
，
）存在两个不相等的“F点”
，
，且
，求a的取值范围.
【答案】（1）①极小值为1，无极大值.②实数k的值为1.（2）
【解析】
（1）①将
代入
可得
，求导讨论函数单调性，即得极值；②设
是函数的一个“F点”（
），即是
的零点，那么由导数
可知
，且
，可得
，根据
可得
，设
，由
的单调性可得，即得
.（2）方法一：先求
的导数，存在两个不相等的“F点”
，
，可以由
和韦达定理表示出，的关系，再由
，可得
的关系式，根据已知解
即得.方法二：由函数存在不相等的两个“F点”和，可知，是关于x的方程组
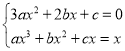的两个相异实数根，由
得
，分两种情况：是函数一个“F点”，不是函数一个“F点”，进行讨论即得.
解：（1）①当时， （
），
则有
（
），令
得
，
列表如下：
x |
| 1 |
|
|
| 0 |
|
|
| 极小值 |
|
故函数在处取得极小值，极小值为1，无极大值.
②设是函数的一个“F点”（）.
（），
是函数的零点.
，由，得
，，
由，得
，即.
设，则
，
所以函数在
上单调增，注意到
，
所以方程存在唯一实根1，所以
，得，
根据①知，时，是函数的极小值点，
所以1是函数的“F点”.
综上，得实数k的值为1.
（2）由
（a，b，
，
），
可得
（）.
又函数存在不相等的两个“F点”和，
，是关于x的方程
（）的两个相异实数根.
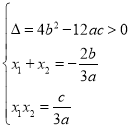
又
，
，
，即
，
从而
，
，
即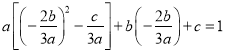
.
.
，
，
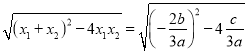
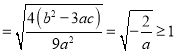解得
.所以，实数a的取值范围为.
（2）（解法2）因为（ a，b，，）
所以（）.
又因为函数存在不相等的两个“F点”和，
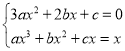所以，是关于x的方程组的两个相异实数根.
由得，
.
（2.1）当是函数一个“F点”时，
且
.
所以
，即
.
又
，
所以
，所以
.又，所以.
（2.2）当不是函数一个“F点”时，
则，是关于x的方程
的两个相异实数根.
又，所以
得
所以
，得
.
所以
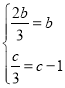，得.
综合（2.1）（2.2），实数a的取值范围为.
