题目内容
已知函数f(x)是实数集R上的奇函数,当x>0时,f(x)=2x+x-1.
(1)求f(-1)的值;
(2)求函数f(x)的表达式.
(1)求f(-1)的值;
(2)求函数f(x)的表达式.
分析:(1)利用奇函数的性质f(-1)=-f(1),即可得出;
(2)当x<0时,则-x>0,利用已知可得:f(-x)=2-x+(-x)-1,又f(-x)=-f(x),可得当x<0时,f(x)=-2-x+x+1;而f(0)=0,
从而得出函数f(x)的解析式.
(2)当x<0时,则-x>0,利用已知可得:f(-x)=2-x+(-x)-1,又f(-x)=-f(x),可得当x<0时,f(x)=-2-x+x+1;而f(0)=0,
从而得出函数f(x)的解析式.
解答:解:(1)∵当x>0时,f(x)=2x+x-1.∴f(1)=2
∵函数f(x)是实数集R上的奇函数,∴f(-x)=-f(x),
∴f(-1)=-f(1)=-2.
(2)由(1)知f(-x)=-f(x).
取x=0,得f(0)=-f(0),∴f(0)=0.
当x<0时,则-x>0,∴f(-x)=2-x+(-x)-1.
又f(-x)=-f(x),∴当x<0时,f(x)=-2-x+x+1.
综上得:f(x)=
∵函数f(x)是实数集R上的奇函数,∴f(-x)=-f(x),
∴f(-1)=-f(1)=-2.
(2)由(1)知f(-x)=-f(x).
取x=0,得f(0)=-f(0),∴f(0)=0.
当x<0时,则-x>0,∴f(-x)=2-x+(-x)-1.
又f(-x)=-f(x),∴当x<0时,f(x)=-2-x+x+1.
综上得:f(x)=
|
点评:本题考查了奇函数的性质和分段函数的意义,属于基础题.

练习册系列答案
相关题目
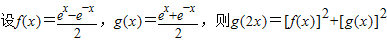 .
.