题目内容
6.如图流程图输出的结果是7.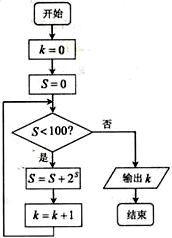
分析 模拟执行程序框图,依次写出每次循环得到的S,k的值,当S=127时不满足条件S<100,退出循环,输出k的值为7.
解答 解:模拟执行程序框图,可得
k=0,S=0
满足条件S<100,S=1,k=1
满足条件S<100,S=3,k=2
满足条件S<100,S=7,k=3
满足条件S<100,S=15,k=4
满足条件S<100,S=31,k=5
满足条件S<100,S=63,k=6
满足条件S<100,S=127,k=7
不满足条件S<100,退出循环,输出k的值为7,
故答案为:7.
点评 本题主要考查了循环结构的程序框图,正确依次写出每次循环得到的S,k的值是解题的关键,属于基础题.

练习册系列答案
相关题目
17.图中所示算法流程图的功能是( )


| A. | 求a、b、c三数的最大数 | B. | 求a、b、c三数的最小数 | ||
| C. | 将a、b、c三数由大到小排列 | D. | 将a、b、c三数由小到大排列 |
14.已知点P(x,y)是直线x+3y-2=0上的动点,则代数式2x+3×8y有( )
| A. | 最小值2$\sqrt{3}$ | B. | 最大值2$\sqrt{3}$ | C. | 最小值4$\sqrt{3}$ | D. | 最大值4$\sqrt{3}$ |
11.过双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左焦点F作圆x2+y2=a2的切线,交y轴于点P,若|OF|=2|OP|,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
18.在△ABC中,若∠A=60°,∠B=45°,BC=3$\sqrt{2}$,则AC等于( )
| A. | 4$\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
15.△ABC外接圆的圆心O,半径为1,若$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AO}$,且|$\overrightarrow{AC}$|=|$\overrightarrow{AO}$|,则向量$\overrightarrow{BA}$在$\overrightarrow{BC}$方向上的投影为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{3}{2}$ |
16.已知函数y=f(x)是定义域为R的奇函数.当x≥0时f(x)=$\left\{{\begin{array}{l}{{x^2},0≤x≤1}\\{f(x-1)+1,x>1}\end{array}}\right.$.若恰有5个不同的实数x1,x2,…,x5,使得f(x)=mx成立,则实数m的值为( )
| A. | $\sqrt{2}$-1 | B. | 2$\sqrt{2}$-2 | C. | 2-$\sqrt{2}$ | D. | 3-2$\sqrt{2}$ |