题目内容
对于函数f(x),若在其定义域内存在两个实数a,b(a<b),使当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“科比函数”.
(1)给出下列两个函数:① ;②
;② ,其中是“科比函数”的函数序号是 ② .
,其中是“科比函数”的函数序号是 ② .
(2)若函数 是“科比函数”,则实数k的取值范围是
是“科比函数”,则实数k的取值范围是 .
.
【答案】
(1)② .
(2) .
.
【解】(1)因为 是增函数,若f(x)为“科比函数”,则f(a)=a,f(b)=b,即
是增函数,若f(x)为“科比函数”,则f(a)=a,f(b)=b,即
a+1=a,b+1=b,无解,所以 不是“科比函数”.
不是“科比函数”.
因为当x∈[0,1]时, ∈[0,1],所以
∈[0,1],所以 是“科比函数”.
是“科比函数”.
(2)因为 是增函数,若
是增函数,若 是“科比函数”,则存在实数a,b(-2≤a<b),使
是“科比函数”,则存在实数a,b(-2≤a<b),使 ,即
,即 .所以a,b为方程
.所以a,b为方程 的两个实数根,从而方程
的两个实数根,从而方程 有两个不等实根.
有两个不等实根.
令 ,则
,则 .当t=0时,k=-2;当t=
.当t=0时,k=-2;当t= 时,k=
时,k= .
.
由图可知,当 时,直线y=k与曲线
时,直线y=k与曲线 有两个不同交点,即方程
有两个不同交点,即方程 有两个不等实根,故实数k的取值范围是
有两个不等实根,故实数k的取值范围是 .
.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
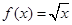 的等域区间是 .
的等域区间是 .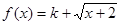 是布林函数,则实数k的取值范围是
.
是布林函数,则实数k的取值范围是
.