题目内容

在三棱锥P-ABC中，PA=PB=PC，BC=2a，AC=a，AB=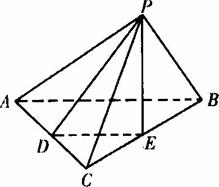a，点P到平面ABC的距离为a.

(Ⅰ)求证：平面PBC⊥平面ABC；

(Ⅱ)求二面角P-AC-B的大小；

(Ⅲ)求点B到平面PAC的距离.

答案：(I)由已知,△ABC为Rt△,∠BAC=90°.

∵PA=PB=PC.∴点P在平面ABC上的射影是斜线BC的中点E.

∴平面PBC⊥平面ABC；

 (Ⅱ)取AC的中点,D,连接PD、PE、DE.

∵PE⊥平面ABC,DE上AC于D,(DE∥AB)

∴AC上PD.∴∠PDE为二面角P—AC—B的平面角. 

∴tan∠PDE=.∵∠PDE=60°.

故二面角P-AC-B为60°.

(Ⅲ)∵PD=S△PAC=.

设点B到平面PAC的距离为d.由VF-ABC=VB-PAC

得S△ABC·PE=S△PAC·d.

∴

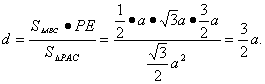
(也可以用向理法求解,略).

练习册系列答案
相关题目
如图，在三棱锥P-ABC中，PA=PB=AB=
2
PC=
2
AC=
2
BC．
（Ⅰ）求证：PA⊥BC； 
（Ⅱ）求二面角P-AB-C所成角的余弦值．
在三棱锥P-ABC中，AB=3，BC=4，AC=5，PA=1  面PAB⊥面CAB，面PAC⊥面CAB，则三棱锥P-ABC的体积是（　　）
精英家教网在三棱锥P-ABC中，PA⊥平面ABC．
（1）若∠BAC=
π3
，AB=AC=PA=2，E、F分别为棱AB、PC的中点，求线段EF的长；
（2）求证：“∠PBC=90°”的充要条件是“平面PBC⊥平面PAB”．
（2013•蚌埠二模）如图，在三棱锥P-ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D，E分别为AB，AC中点．
（I）求证：DE∥面PBC；
（II）求证：AB⊥PE；
（III）求三棱锥B-PEC的体积．
如图，在三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC上一点，它的正（主）视图和侧（左）视图如图所示．
（1）证明：AD⊥平面PBC；
（2）求三棱锥D-ABC的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网