题目内容
设命题P：|m|≤1，命题q：方程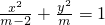
表示的曲线是双曲线．若p∨q为真，p∧q为假，求实数m的取值范围．
解：命题P：|m|≤1，为真命题，则-1≤m≤1
命题q：方程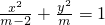表示的曲线是双曲线，为真命题，则m（m-2）＜0，∴0＜m＜2
∵p∨q为真，p∧q为假，∴p与q一真一假，
①p真q假，则
，∴-1≤m≤0；
②p假q真，则
，∴1＜m＜2
综上知，实数m的取值范围为[-1，0]∪（1，2）
分析：首先分别求出命题为真时，参数的范围，再根据p∨q为真，p∧q为假，判断出p与q一真一假，对于两个命题的一真一假进行讨论，即可求得实数m的取值范围．
点评：本题考查命题的真假与应用，是一个中档题目，解题的关键是根据p∨q为真，p∧q为假，判断出p与q一真一假．
命题q：方程
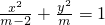表示的曲线是双曲线，为真命题，则m（m-2）＜0，∴0＜m＜2∵p∨q为真，p∧q为假，∴p与q一真一假，
①p真q假，则
，∴-1≤m≤0；②p假q真，则
，∴1＜m＜2综上知，实数m的取值范围为[-1，0]∪（1，2）
分析：首先分别求出命题为真时，参数的范围，再根据p∨q为真，p∧q为假，判断出p与q一真一假，对于两个命题的一真一假进行讨论，即可求得实数m的取值范围．
点评：本题考查命题的真假与应用，是一个中档题目，解题的关键是根据p∨q为真，p∧q为假，判断出p与q一真一假．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
+
=1表示的图象是双曲线；命题q：?x∈R，3x2+2mx+（m+6）＜0．求使“p且q”为真命题时，实数m的取值范围．
+
=1表示焦点在y轴上的椭圆，命题q：当0＜x＜2时，函数f（x）=x+
＞m恒成立．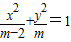
表示的曲线是双曲线．若p∨q为真，p∧q为假，求实数m的取值范围．