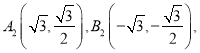题目内容
【题目】已知函数
，（ 
）满足：①
；②
.
（1）求
的值；
（2）若对任意的实数
，都有
成立，求实数
的取值范围.
【答案】(1)a＝1，c＝2；(2) 
.
【解析】试题分析：（1）根据条件代入二次函数的解析式，求出
的值；（2）转化为二次函数求最小值小于等于零恒成立，或利用分离参数的方法求m的取值范围.
试题解析：(1)∵f(1)＝a＋2＋c＝5，∴c＝3－a.①
又∵6＜f(2)＜11，即6＜4a＋c＋4＜11，②
将①式代入②式，得
又∵a、c∈N*，∴a＝1，c＝2.
(2)由(1)知f(x)＝x2＋2x＋2.
法一：设g(x)＝f(x)－2mx＝x2＋2(1－m)x＋2.
当
，即
， 
，故只需
，
解得
，又∵
，故无解.
当
，即
时， 
，故只需
，解得
，
又
，∴
.
综上可知， 
的取值范围是
.
法二：∵
，∴不等式
恒成立
在
上恒成立，
易知
，故只需
即可，解得
.
练习册系列答案
相关题目
