题目内容
如图,F1,F2是离心率为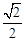 的椭圆C:
的椭圆C: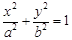 (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线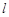 :x=-
:x=-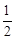 将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
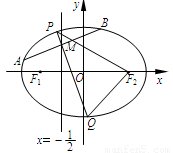
(Ⅰ) 求椭圆C的方程;
(Ⅱ) 求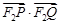 的取值范围.
的取值范围.
【答案】
(Ⅰ)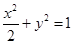 ;(Ⅱ)
;(Ⅱ)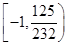 .
.
【解析】
试题分析:(Ⅰ)根据题中的已知条件列有关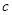 的方程,求出
的方程,求出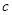 ,然后根据离心率求出
,然后根据离心率求出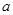 ,最后再根据
,最后再根据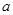 、
、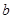 、
、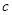 三者之间的关系求出
三者之间的关系求出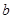 的值,从而确定椭圆
的值,从而确定椭圆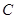 的方程;(Ⅱ)先设点
的方程;(Ⅱ)先设点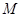 的坐标
的坐标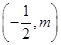 ,然后根据已知条件将直线
,然后根据已知条件将直线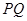 的方程用
的方程用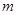 进行表示,再联立直线
进行表示,再联立直线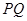 与椭圆
与椭圆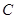 的方程,结合韦达定理将
的方程,结合韦达定理将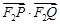 表示为含
表示为含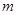 为代数式,然后再利用不等式的性质求出
为代数式,然后再利用不等式的性质求出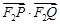 的取值范围.
的取值范围.
试题解析:(Ⅰ)设F2(c,0),则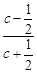 =
=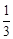 ,所以c=1.
,所以c=1.
因为离心率e=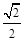 ,所以a=
,所以a=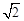 .
.
所以椭圆C的方程为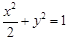 .
.
(Ⅱ) 当直线AB垂直于x轴时,直线AB方程为x=-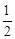 ,此时P(
,此时P(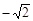 ,0)、Q(
,0)、Q(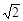 ,0),
,0),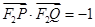 .
.
当直线AB不垂直于x轴时,设直线AB的斜率为k,M(-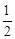 ,m) (m≠0),A(x1,y1),B(x2,y2).
,m) (m≠0),A(x1,y1),B(x2,y2).
由 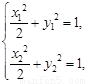 得(x1+x2)+2(y1+y2)
得(x1+x2)+2(y1+y2) =0,
=0,
则-1+4mk=0,故k=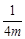 .
.
此时,直线PQ斜率为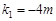 ,PQ的直线方程为
,PQ的直线方程为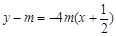 .即
.即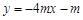 .
.
联立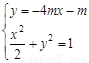 消去y,整理得
消去y,整理得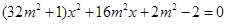 .
.
所以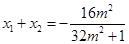 ,
,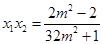 .
.
于是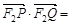 (x1-1)(x2-1)+y1y2
(x1-1)(x2-1)+y1y2
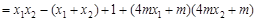

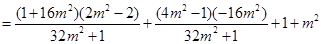
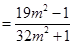 .
.
令t=1+32m2,1<t<29,则 .
.
又1<t<29,所以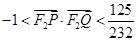 .
.
综上,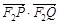 的取值范围为
的取值范围为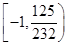 .
.
考点:椭圆的方程、平面向量的数量积、韦达定理

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 如图,F1,F2是离心率为
如图,F1,F2是离心率为 (2013•浙江模拟)如图,F1,F2是离心率为
(2013•浙江模拟)如图,F1,F2是离心率为 的椭圆C:
的椭圆C: (a>b>0)的左、右焦点,直线:x=-
(a>b>0)的左、右焦点,直线:x=- 将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
 的取值范围.
的取值范围. 的椭圆
的椭圆 (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线 :x=-
:x=- 将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中点M在直线l上,线段AB的中垂线与C交于P,Q两点.
将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中点M在直线l上,线段AB的中垂线与C交于P,Q两点.
 的椭圆C:
的椭圆C: (a>b>0)的左、右焦点,直线
(a>b>0)的左、右焦点,直线 :x=-
:x=- 将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
将线段F1F2分成两段,其长度之比为1 : 3.设A,B是C上的两个动点,线段AB的中垂线与C交于P,Q两点,线段AB的中点M在直线l上.
 的取值范围.
的取值范围.