题目内容
已知f(x)是定义在(-∞,+∞)上的函数,m、n∈(-∞,+∞),请给出能使命题:“若m+n>0,则f(m)+f(n)>f(-m)+f(-n)”成立的一个充分条件.
思路分析:要找命题q:若m+n>0,则f(m)+f(n)>f(-m)+f(-n)的一个充分条件就是要找一个命题p满足p![]() q,这样的命题p易找到,且不唯一.
q,这样的命题p易找到,且不唯一.
解:当f(x)为增函数时,由m+n>0得m>-n,∴f(m)>f(-n).同理可得f(n)>f(-m).于是有f(m)+f(n)>f(-m)+f(-n).
故使命题成立的一个充分条件是f(x)为R上的单调递增函数,如f(x)=ax+b(a>0),f(x)=2x+3等等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ) =
f(x)-f(y)
) =
f(x)-f(y) 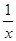 ) <2
) <2  ∪
∪ 上的奇函数,当
上的奇函数,当 时,f (x)的图象如图所示,那么f (x)的值域是
时,f (x)的图象如图所示,那么f (x)的值域是
