题目内容
已知数列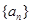 ,
,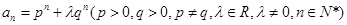 .
.
(1)求证:数列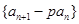 为等比数列;
为等比数列;
(2)数列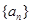 中,是否存在连续的三项,这三项构成等比数列?试说明理由;
中,是否存在连续的三项,这三项构成等比数列?试说明理由;
(3)设 ,其中
,其中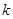 为常数,且
为常数,且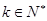 ,
,
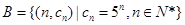 ,求
,求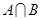 .
.
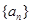 ,
,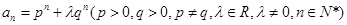 .
.(1)求证:数列
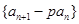 为等比数列;
为等比数列;(2)数列
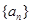 中,是否存在连续的三项,这三项构成等比数列?试说明理由;
中,是否存在连续的三项,这三项构成等比数列?试说明理由;(3)设
 ,其中
,其中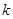 为常数,且
为常数,且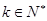 ,
,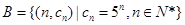 ,求
,求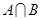 .
. 解:⑴∵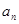 =
=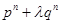 ,∴
,∴
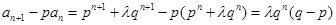 ,
,
∵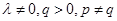 ∴
∴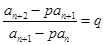 为常数∴数列
为常数∴数列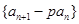 为等比数列
为等比数列
⑵取数列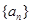 的连续三项
的连续三项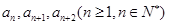 ,
,
∵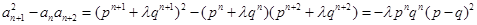 ,
,
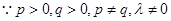 ,∴
,∴ ,即
,即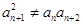 ,
,
∴数列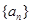 中不存在连续三项构成等比数列;
中不存在连续三项构成等比数列;
⑶当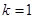 时,
时,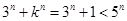 ,此时
,此时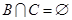 ;
;
当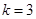 时,
时,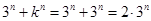 为偶数;而
为偶数;而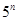 为奇数,此时
为奇数,此时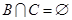 ;
;
当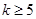 时,
时,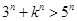 ,此时
,此时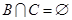 ;
;
当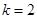 时,
时,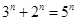 ,发现
,发现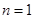 符合要求,下面证明唯一性(即只有
符合要求,下面证明唯一性(即只有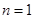 符合要求)。
符合要求)。
由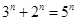 得
得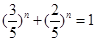 ,
,
设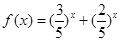 ,则
,则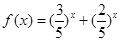 是
是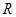 上的减函数,∴
上的减函数,∴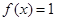 的解只有一个
的解只有一个
从而当且仅当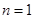 时
时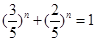 ,即
,即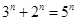 ,此时
,此时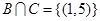 ;
;
当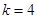 时,
时,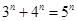 ,发现
,发现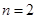 符合要求,下面同理可证明唯一性(即只有
符合要求,下面同理可证明唯一性(即只有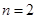 符合要求)。
符合要求)。
从而当且仅当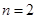 时
时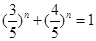 ,即
,即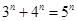 ,此时
,此时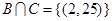 ;
;
综上,当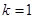 ,
,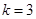 或
或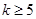 时,
时,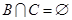 ;
;
当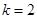 时,
时,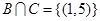 ,
,
当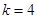 时,
时,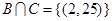 。
。
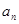 =
=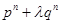 ,∴
,∴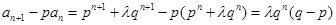 ,
,∵
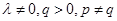 ∴
∴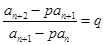 为常数∴数列
为常数∴数列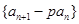 为等比数列
为等比数列⑵取数列
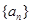 的连续三项
的连续三项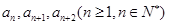 ,
,∵
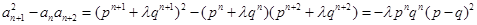 ,
,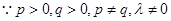 ,∴
,∴ ,即
,即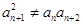 ,
,∴数列
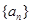 中不存在连续三项构成等比数列;
中不存在连续三项构成等比数列; ⑶当
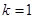 时,
时,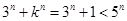 ,此时
,此时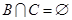 ;
;当
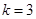 时,
时,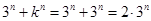 为偶数;而
为偶数;而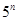 为奇数,此时
为奇数,此时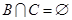 ;
;当
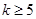 时,
时,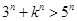 ,此时
,此时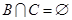 ;
;当
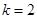 时,
时,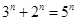 ,发现
,发现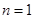 符合要求,下面证明唯一性(即只有
符合要求,下面证明唯一性(即只有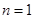 符合要求)。
符合要求)。由
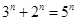 得
得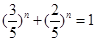 ,
,设
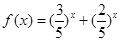 ,则
,则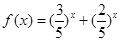 是
是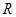 上的减函数,∴
上的减函数,∴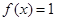 的解只有一个
的解只有一个从而当且仅当
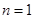 时
时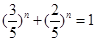 ,即
,即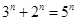 ,此时
,此时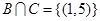 ;
;当
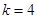 时,
时,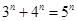 ,发现
,发现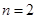 符合要求,下面同理可证明唯一性(即只有
符合要求,下面同理可证明唯一性(即只有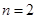 符合要求)。
符合要求)。从而当且仅当
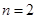 时
时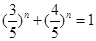 ,即
,即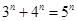 ,此时
,此时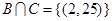 ;
;综上,当
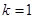 ,
,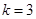 或
或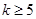 时,
时,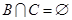 ;
;当
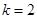 时,
时,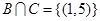 ,
,当
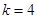 时,
时,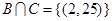 。
。 略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
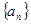 中,各项都是正数,且
中,各项都是正数,且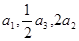 成等差数列,则
成等差数列,则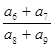 等
等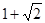 B
B 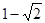 C
C 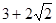 D
D 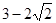
 这个厂的总产值为___________.
这个厂的总产值为___________. 为等比数列
为等比数列 的前
的前 项和,
项和, ,则
,则



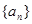 中,
中,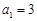 ,前三项和为21,则
,前三项和为21,则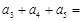 ( )
( )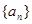 中,
中,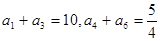 ,则等比数列
,则等比数列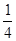
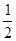
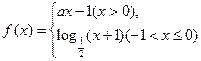 且
且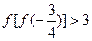 ,在各项为正的数列
,在各项为正的数列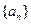 中,
中,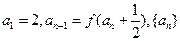 的前n项和为
的前n项和为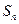 ,若
,若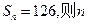 = 。
= 。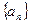 中,已知
中,已知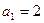 ,
,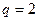 ,
,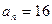 ,则项数
,则项数 .
.
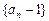 是等比数列,且
是等比数列,且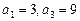 ,
,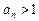
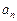
 的表达式;
的表达式;  .
.