题目内容
(2013•南充三模)已知正项等比数列{an}满足a7=a6+2a5,若存在两项am、an使得
=2a1,则mn的最大值是
| aman |
4
4
.分析:把所给的数列的三项之间的关系,写出用第五项和公比来表示的形式,求出公比的值,整理所给的条件,写出m,n之间的关系,用基本不等式得到最小值.
解答:解:∵a7=a6+2a5,
∴a5q2=a5q+2a5,
∴q2-q-2=0,
∴q=2,
∵存在两项am,an使得
=2a1
∴aman=4a12,
∴qm+n-2=4,
∴m+n=4
∴mn≤(
)2=4
当且仅当m=n时即m=2,n=2时取得等号
∴mn的最大值是4.
故答案为:4.
∴a5q2=a5q+2a5,
∴q2-q-2=0,
∴q=2,
∵存在两项am,an使得
| aman |
∴aman=4a12,
∴qm+n-2=4,
∴m+n=4
∴mn≤(
| m+n |
| 2 |
当且仅当m=n时即m=2,n=2时取得等号
∴mn的最大值是4.
故答案为:4.
点评:本题考查等比数列的通项和基本不等式,实际上应用基本不等式是本题的重点和难点,属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 (2013•南充三模)M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.
(2013•南充三模)M公司从某大学招收毕业生,经过综合测试,录用了14名男生和6名女生,这20名毕业生的测试成绩如茎叶图所示(单位:分),公司规定:成绩在180分以上者到“甲部门”工作;180分以下者到“乙部门”工作.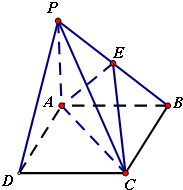 (2013•南充三模)如图,在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4
(2013•南充三模)如图,在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,PA⊥平面ABCD,E为PB中点,PB=4 (2013•南充三模)如图是一个空间几何体的三视图,这个几何体的体积是( )
(2013•南充三模)如图是一个空间几何体的三视图,这个几何体的体积是( )