题目内容
【题目】设![]() ,函数
,函数![]() .
.
(1)若![]() ,求
,求![]() 的反函数
的反函数![]() ;
;
(2)求函数![]() 的最大值(用
的最大值(用![]() 表示);
表示);
(3)设![]() ,若对任意
,若对任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的范围.
的范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)根据反函数定义求解即可;
(2)根据y=f(x)f(﹣x),判断函数y的单调性即可求解最大值.
(3)g(x)=f(x)﹣f(x﹣1)![]() ,换元t=a2x,得h(t)
,换元t=a2x,得h(t)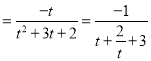 ,讨论
,讨论![]() 和
和![]() 时,h(t)最值即可求解
时,h(t)最值即可求解
(1)当a=1时,f(x)![]() ,
,
∴1+2x![]() ,
,
即2x![]() 1
1![]() ,则0<y<1,
,则0<y<1,
∴x=log2(![]() );
);
故f(x)的反函数f﹣1(x)=log2(![]() ),x∈(0,1)
),x∈(0,1)
(2)∵y=f(x)f(﹣x)![]()
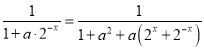 ,
,
设y=2x+2﹣x,易知,函数y=2x+2﹣x在(﹣∞,0)上单调递减,在(0,+∞)上单调递增,
则当x=0时,y=2x+2﹣x有最小值,最小值为2,
∴当x=0时,y=f(x)f(﹣x)有最大值,
∴ymax![]() ;
;
(3)g(x)=f(x)﹣f(x﹣1)![]() ,令t=a2x,∵x∈(﹣∞,0],a>0,∴0<t≤a.
,令t=a2x,∵x∈(﹣∞,0],a>0,∴0<t≤a.
∴h(t)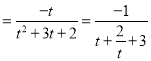 ,
,
当![]() 时h(t)在(0,a]上单调递减,所以
时h(t)在(0,a]上单调递减,所以![]()
∵对任意x∈(﹣∞,0],g(x)≥g(0)恒成立,且g(0) ,
,
∴ 恒成立,∴0
恒成立,∴0![]()
当![]() 时,
时, ,令
,令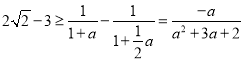 不恒成立,舍去
不恒成立,舍去
综上,a的取值范围是(0,![]() ].
].

【题目】辽宁省六校协作体(葫芦岛第一高中、东港二中、凤城一中、北镇高中、瓦房店高中、丹东四中)中的某校理科实验班的100名学生期中考试的语文、数学成绩都不低于100分,其中语文成绩的频率分布直方图如图所示,成绩分组区间是:[100,110),[110,120),[120,130),[130,140),[140,150].
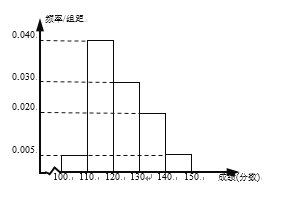
这100名学生语文成绩某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示:
之比如下表所示:
分组区间 | [100,110) | [110,120) | [120,130) | [130,140) |
| 1:2 | 2:1 | 3:4 | 1:1 |
(1)估计这100名学生语文成绩的平均数、方差(同一组数据用该区间的中点值作代表);
(2)从数学成绩在[130,150] 的学生中随机选取2人,该2人中数学成绩在[140,150]的人数为![]() ,求
,求![]() 的数学期望
的数学期望![]() .
.