题目内容
 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=4,∠BCE=60°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=4,∠BCE=60°.(1)证明:平面BAE⊥平面DAE;
(2)点P为线段AB上一点,求直线PE与平面DCE所成角的取值范围.
分析:(1)取BE的中点O,连OC,OF,DF,可利用条件得OC∥FD,再利用条件证得OC⊥平面ABE即可得到平面ADE⊥平面ABE;
(2)以0为原点建立空间直角坐标系O-xyz,设出P点的坐标,分别求出直线PE的方向向量与平面DCE的法向量,代入向量夹角公式,求出直线PE与平面DCE所成角正弦值的取值范围,进而可以确定直线PE与平面DCE所成角的取值范围.
(2)以0为原点建立空间直角坐标系O-xyz,设出P点的坐标,分别求出直线PE的方向向量与平面DCE的法向量,代入向量夹角公式,求出直线PE与平面DCE所成角正弦值的取值范围,进而可以确定直线PE与平面DCE所成角的取值范围.
解答: 解:(1)证明:取BE的中点O,连OC,OF,DF,则2OF与BA平行且相等(2分)
解:(1)证明:取BE的中点O,连OC,OF,DF,则2OF与BA平行且相等(2分)
∵AB⊥平面BCE,CD⊥平面BCE,∴2CD与BA平行且相等,
∴OF与CD平行且相等,
∴OC∥FD(4分)
∵BC=CE,∴OC⊥BE,又AB⊥平面BCE.
∴OC⊥平面ABE.∴FD⊥平面ABE.
从而平面ADE⊥平面ABE.(6分)
(2)以0为原点建立空间直角坐标系O-xyz,如图,
则已知条件有:C(2
,0,0),D(2
,0,2),E(0,-2,0)
平面DCE的一个法向量记为
=(x,y,z)
则
,即
∴
=(1,-
,0)…9分
令直线PE与平面DCE所成角为θ
设P(0,2,Z),(0≤Z≤4)
则sinθ=
=
…11分
∵0≤Z≤4
∴
≤
≤
∴直线PE与平面DCE所成角的范围为[arcsin
,
]…12分
 解:(1)证明:取BE的中点O,连OC,OF,DF,则2OF与BA平行且相等(2分)
解:(1)证明:取BE的中点O,连OC,OF,DF,则2OF与BA平行且相等(2分)∵AB⊥平面BCE,CD⊥平面BCE,∴2CD与BA平行且相等,
∴OF与CD平行且相等,
∴OC∥FD(4分)
∵BC=CE,∴OC⊥BE,又AB⊥平面BCE.
∴OC⊥平面ABE.∴FD⊥平面ABE.
从而平面ADE⊥平面ABE.(6分)
(2)以0为原点建立空间直角坐标系O-xyz,如图,
则已知条件有:C(2
| 3 |
| 3 |
平面DCE的一个法向量记为
| t |
则
|
|
∴
| t |
| 3 |
令直线PE与平面DCE所成角为θ
设P(0,2,Z),(0≤Z≤4)
则sinθ=
|
| ||||
|
|
2
| ||
|
∵0≤Z≤4
∴
| ||
| 4 |
2
| ||
|
| ||
| 2 |
∴直线PE与平面DCE所成角的范围为[arcsin
| ||
| 4 |
| π |
| 3 |
点评:本题考查的知识点是向量语言表述面面的垂直、平行关系,用空间向量求直线与平面的夹角,其中建立空间坐标系,将空间线面关系及线面夹角问题转化为向量的夹角问题是解答本题的关键.

练习册系列答案
相关题目
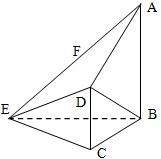 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°,F为AE中点. 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,AB=BC=CE=2CD=2,∠BCE=120°.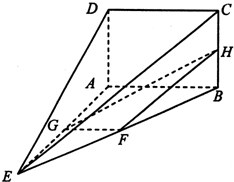 (2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(2013•贵阳二模)如图,在四棱锥E-ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点 (2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE.
(2012•淮南二模)如图,在四棱锥E-ABCD中,四边形ABCD为平行四边形,BE=BC,AE⊥BE,M为CE上一点,且BM⊥面ACE. 如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,
如图,在四棱锥E-ABCD中,AB⊥平面BCE,CD⊥平面BCE,