题目内容
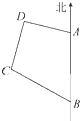 如图,海岸线上有相距5海里的两座灯塔A,B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处.求甲、乙两艘轮船之间的距离.
如图,海岸线上有相距5海里的两座灯塔A,B,灯塔B位于灯塔A的正南方向.海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距3海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处.求甲、乙两艘轮船之间的距离.分析:先连接AC,可得到BC的长度和∠CAD的值,再由余弦定理将题中数据代入即可得到答案
解答:解:连接AC,由题意可知AB=BC=5,∠ABC=∠ACB=∠BAC=60°,∠CAD=45°
根据余弦定理可得CD2=AC2+AD2-2×AC×AD×cos∠CAD
=25+9-2×5×3×
=24-15
所以CD=
海里.
即甲、乙两艘轮船之间的距离为
海里.
根据余弦定理可得CD2=AC2+AD2-2×AC×AD×cos∠CAD
=25+9-2×5×3×
| ||
| 2 |
| 2 |
所以CD=
24-15
|
即甲、乙两艘轮船之间的距离为
24-15
|
点评:本题以实际问题为载体,考查解三角形,主要考查余弦定理的应用.属基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
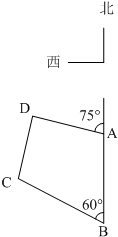 如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距
如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距 如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距
如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距 海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘船之间的距离为 海里.
海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘船之间的距离为 海里. 如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距
如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距 海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘船之间的距离为 海里.
海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘船之间的距离为 海里. 如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距
如图,海岸线上有相距5海里的两座灯塔A、B,灯塔B位于灯塔A的正南方向,海上停泊着两艘轮船,甲船位于灯塔A的北偏西75°方向,与A相距 海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘船之间的距离为 海里.
海里的D处;乙船位于灯塔B的北偏西60°方向,与B相距5海里的C处,则两艘船之间的距离为 海里.